University of Hyderabad (UoH) 2010 Entrance Exams Other Entrance Exams Ph.D Programme Entrance - Mathematics - Question Paper
Ph.D Programme Entrance examination - Mathematics
University of Hyderabad, _ Entrance Examination, 2010 Ph.D. (Mathematics/Applied Mathematics/OR)

Hall Ticket No.
|
Time: 2 hours Part B: 50 |
1 |
a |
b |
c |
d |
|
Instructions 1. Calculators are not allowed. 2. Part A carries 25 marks. Each correct answer carries 1 mark and each wrong answer carries - 0*33 mark. So do not gamble. If you want to change any answer, cross out the old one and circle the new one. Over written answers will be ignored. 3. Part B carries 50 marks. Instructions for answering Part B are given at the beginning of Part B. 4. Use a separate booklet for Part B. |
2 |
a |
b |
c |
d |
|
3 |
a |
b |
c |
d | |
|
4 |
a |
b |
c |
d | |
|
5 |
a |
b |
c |
d | |
|
6 |
a |
b |
c |
d | |
|
7 |
a |
b |
c |
d | |
|
8 |
a |
b |
c |
d | |
|
9 |
a |
b |
c |
d | |
|
10 |
a |
b |
c |
d | |
|
11 |
a |
b |
c |
d | |
|
12 |
a |
b |
c |
d | |
|
13 |
a |
b |
c |
d | |
|
14 |
a |
b |
c |
d | |
|
15 |
a |
b |
c |
d | |
|
16 |
a |
b |
c |
d | |
|
17 |
a |
b |
c |
d | |
|
18 |
a |
b |
c |
d | |
|
a |
b |
c |
d | ||
|
20 |
a |
b |
c |
d | |
|
21 |
a |
b |
c |
d | |
|
22 |
a |
b |
c |
d | |
|
23 |
a |
b |
c |
d | |
|
24 |
a |
b |
c |
d | |
|
25 |
a |
b |
c |
d |
PART A
Each question carries 1 mark.< 0.33 mark will be deducted for each wrong answer. There will be no penalty if the question is left unanswered.
The set of real numbers is denoted by R, the set of complex numbers by C, the set of rational numbers by Q and the set of integers by Z.
1. Let V be a real vector space and S = {vi,v2, .,vk} be a linearly independent subset of V. Then
(a) dim V = k.
(b) dim V < k.
(c) dim V > k.
(d) nothing can be said about dim V.
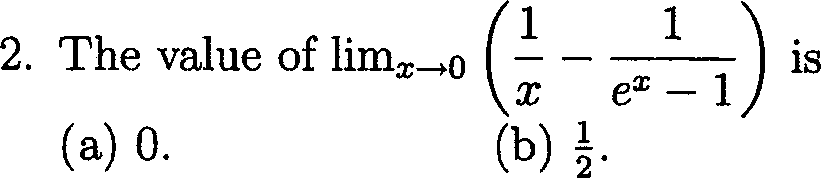
(c) 1.
3. Consider the function f(x) on R defined by
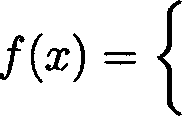 |
f x3, if x2 < 1 \ x, if x2 > 1. |
Then
(a) / is continuous at each point of R.
(b) / is continuous at each point of except at x = 1.
(c) / is differentiable at each point of R.
(d) / is not continuous at any point of R.
4. Let f(x,y) be defined on R2 by f(x,y) = |x| + \y\. Then
(a) the partial derivatives of / at (0,0) exist.
(b) / is differentiable at (0,0).
(c) / is continuous at (0,0).
(d) none of the above hold.
5. Let / : M > M be continuous taking values in Q, the set of rational numbers. Then
(a) / is strictly monotone.
(b) / is unbounded.
(c) / is differentiable.
(d) the image of / is infinite
6. For the set + : m, n G N}, the element | is
(a) both an element in the set and a limit point of the set.
(b) neither an element in the set nor a limit point.
(c) an element in the set, but not a limit point.
(d) a limit point of the set, but not an element in the set.
7. If | tanz| = 1, then
/ \ 7T rwr
(a) Re z = - + .
7r
(b) Re z = + rwr.
4
(c) Re 2: = + nn.
, 7r mr
(d) Re 2 = + .
10. Let (X, d) be a metric sparse and A c X. Then A is totally bounded if
and only if
(a) every sequence in A has a Cauchy subsequence.
(b) every sequence in A has a convergent subsequence.
(c) every sequence in A has a bounded subsequence.
(d) every bounded sequence in A has a convergent subsequence.
11. Suppose N is a normal subgroup of G. For an element a: in a group, let 0(x) denote the order of x. Then
(a) 0(a) divides 0(aN).
(b) O(aN) divides 0(a).
(c) 0(a) 0(aN).
(d) 0(a) = 0(aN).
12. If G is a group such that it has a unique element a of order n. Then
(a) n 2.
(b) n is a prime.
(c) n is an odd prime.
(d) 0(G) = n.
13. Consider the ring Z. Then
(a) all its ideals are prime.
(b) all its non-zero ideals are maximal.
(c) Z/J is an integral domain for any ideal I of Z.
(d) any generator of a maximal ideal in Z is prime.
14. Fn denotes the finite field with n elements. Then
(a) F4 C F8.
(c) F4 C F16.
15. Let A be an n x n matrix which is both Hermitian and unitary. Then
(a) A2 = I.
(b) A is real.
(c) The eigenvalues of A are 0,1, -1.
(d) The minimal and characteristic polynomials are same.
16. For 0 < 6 < 7r, the matrix
/ cos# sin# \ y sin# cosd J
(a) has real eigenvalues.
(b) is symmetric.
(c) is skew-symmetric.
(d) is orthogonal.
17. Let {, v} C i3 be a linearly independent set and let A = {w e R3 :
| |w| | = 1 and {nu, v, w} is linearly independent for some n N}. Then
(a) A is a singleton.
(b) A is finite but not a singleton.
(c) A is countably finite.
(d) A is uncountable.
18. A : A is a 5 x 5 complex matrix of finite order, that is, Ak I for some k E N, must be diagonalizable.
B : A diagonalizable 5x5 matrix must be of finite order.
Then
(a) A and B are both true.
(b) A is true but B is false.
(c) B is true but A is false.
(d) Both A and B are false.
19. Let V C7[0,1] be the vector space of continuous functions on [0,1]. Let \\f\h = fo 1/(01* and H/IU := sup{|/(t)| : 0 < t < 1}. Then
(a) (V,|| ||i) and (V,|| ||
OO ) are Banach spaces.
(b) (V,||||
OO
) is complete but (V, || j|i) is not.
(c) (V, || ||i) is complete but (V. || H) is not.
(d) Neither of the spaces (V, || Hi), (V, || H) are complete.
20. The space lp is a Hilbert space if and only if
(a) p > 1. (b) p is even. (c) p = oo. (d) p = 2.
21. Which of the following statements is correct?
(a) On every vector space V over R or C, there is a norm with respect to which V is a Banach space.
(b) If (X,\\.\\) is a normed space and Y is a subspace of X, then every bounded linear functional f0 on Y has a unique bounded linear extension / to X such that ||/|| = ||/0||.
(c) Dual of a separable Banach space is separable.
(d) A finite dimensional vector space is a Banach space with respect to any norm on it.
24. The set of all eigenvalues of the Sturm-Liouville problem
y" + Ay = 0, y'(0) = 0, y'(|) = 0
is given by
(a) A 0, A = 2n, n = 1,2,3,____
(b) A 7 0, A 4n2, n 1,2,3,____
(c) A = 2n, n = 0,1,2,3,....
25. A complete integral of zpq = p2q(x + q) +pq2(y + p) is
(a) z = ax + by 2ab.
(b) xz = ax by + 2ab.
(c) xz = by ax + 2ab.
(d) xz = ax + by + 2ab.
PART B
Answer any ten questions. Each question carries 5 marks.
1. List all possible Jordan Canonical forms of a 7 x 7 real matrix whose minimal polynomial is (x - l)2(re - 2)(x + 3) and characteristic polynomial is (x - l)2 (a: - 2)2(x + 3)3.
2. A is an m x n matrix and B is an n x m matrix, n < m, then prove that AB is never invertible.
3. Let / : C C be a non-constant entire function with the point at infinity as a pole. Show that / is a polynomial.
4. Show that L2([0,1]) C i,x([0,1]) and the inclusion map / - / from L2[0,1] to #[0,1] is a bounded linear operator.
5. Let / : (C > C be a complex analytic function such that f(f{z)) for all z C with \z\ = 1. Show that / is either constant or identity.
6. Let p{x) = anxn + an-ixn~1 + + a\X + ao be a polynomial whose co-efficients satisfy 2= o m = 0- Then p(x) has a real root between 0
and 1.
7. Give an example of a decreasing sequence {/} of measurable functions defined on a measurable set E of E such that fn*f pointwise a.e. on E but fEf limn_+00 fE fn.
8. Show that all 3-Sylow subgroups in Si are conjugate.
9. Let a be algebraic over a field K such that the degree [K{a) : K] is odd. Show that K(a) = K(a2).
2 2
10. Let E be the ellipse + p- = 1, H be the hyperbola xy = 1 and P be the parabola y = x2. Show that no two of these are homeomorphic.
11. Verify whether
Qi Q1Q2, Q2 Qi + Q2
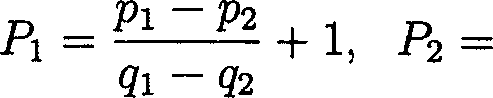 |
(I2P2 ~ QiPi 92-9i |
(92 + 9i),
is a canonical transformation for a system having two degrees of freedom.
12. Determine the Greens function for the boundary value problem
xy" + y' = -fix), \<x<oo
2/(1) = 0, lim \y(x)\ < oo
XOO
13. Find the critical point of the system
ax n dy
= z + y-2xy, -
and discuss its nature and stability.
2x + y + 3y2,
14. Reduce the following partial differential equation to a canonical form and solve, if possible.
xx 2X1Lxy 1 "Uyy ILy.
15. Determine the two solutions of the equation pq = 1 passing through the straight line C : x0 2s, y0 = 2s, z0 5s.
16. Let x denote the optimal solution to the following linear programming problem PI :
min cTx s.t. Ax > b x > 0,
where A E Mmxn , b G Rm and c, x Rn. Now, a new constraint aTx > (3, where a G Rn and (3 G R, is added to the feasible region and we get the following linear programming problem P2 :
min cTx s.t. Ax > b aTx > 0 x > 0.
Discuss about the optimality of x for the two cases (a) x is feasible to the new LP (P2) and (b) x is not feasible to the new LP (P2).
17. Consider the following linear programming problem
min xi + x2
s.t. sxi + tx2 > 1
> 0
X2 unrestricted.
Find conditions on s and t to make the linear programming problem have (a) multiple optimal solutions and (b) an unbounded solution.
18. Five employees are available for four jobs in a firm. The time (in minutes) taken by each employee to complete each job is given in the table below.
|
PersonJ, Job |
1 |
2 |
3 |
4 |
|
1 |
24 |
18 |
32 |
18 |
|
2 |
20 |
- |
29 |
24 |
|
3 |
28 |
22 |
30 |
30 |
|
4 |
18 |
24 |
- |
16 |
|
5 |
23 |
- |
27 |
29 |
The objective of the firm is to assign employees to jobs so as to minimize the total time taken to perform the four jobs. Dashes indicate a person cannot do a particular job.
(a) Formulate the above problem as a linear programming problem and state the Dual of the problem.
(b) What is the optimal assignment to the problem?
9
|
Attachment: |
| Earning: Approval pending. |
