Indian Institute of Technology Guwahati (IIT-G) 2007 JAM Computer Applications - Question Paper
JAM 2007 Computer Aplpications
Full ques. Paper in attachment
Computer Applications Paper
2007
Special Instructions / Useful Data
N denotes the set of natural numbers.
Z denotes the set of integers.
Q denotes the set of rational numbers.
R denotes the set of real numbers.
PT denotes the transpose of a matrix P. x denotes the complement of a Boolean variable x. f' denotes the derivative of a function /.
denotes the partial derivative of z with respect to x. dx V
E(X) denotes the expected value of a random variable X.
R3 = {xr = (xj, x2, x3): xv x2, x3 e r}
Z = {0,1, 2, , n-l}
denotes addition modulo n.
All bold faced vectors are column vectors.
For all C programs assume that all standard library functions are accessible.
F(x) = J(i-l)(f-2)(f-3)(f-4)tft, 0<*<5.
o
Then F has local minimum at the points
(A) {0,2,4}
(B) {1,3,5}
j
j
(C) {0,3,4}
(D) {3,4,5}
The integral
2.
71
2
j"min (sinx, cosx)dx
o
equals
(A) V2-2
(B) 2-V2
(D) 2 + V2 *
For n > 5 , the expression
1 + 2* + 3x2 +4x3 +--- + nxn~1, x*l, is equal to
nxn (l jc) jc71 +1
(A)
.2
nxn (x -1) - xn +1
h \2 (1-x)
nx11 (x -1) + xn -1
(1 \2 {1-x)
nxn
(D) /, V (1-x)
4. The function /defined on R by
/(x) = 3x+4*-5x
has
(A) exactly one zero
(B) exactly two zeros
(C) exactly three zeros
(D) infinitely many zeros
5. The spheres
x2 + y2 + z2 = 1 and x2 + (y-Vi}) +z2 =4
intersect at an angle
(A) 0
(B)
n
6
(C)
n
4
6. If Q denotes the region bounded by the X-axis and the lines y = x and x = 1, then the value of the integral
(D) sin 2
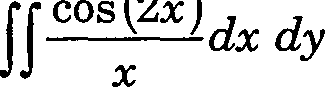 |
|
a |
|
is |
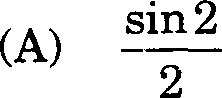 |
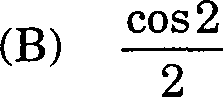 |
|
(C) cos2 |
7. Let f be an increasing, differentiable function. If the curve y = f{x) passes through (l, l) and has length
1
then the curve is
(A) y = ln(Vx)-l
(B) y = l-ln(Vx)
(C) y = ln(l + Vx)
(D) y = l + ln(\/x)
8. If the line y = mx, 0 < x < 2 is rotated about the line y = -1, then the area of the generated surface is
(A) 4r(l+ /n)Vl + m
(D) 4(l + 7n)Vl + m2
9. Let D be the region in the first quadrant lying between x2 +y2 = 1 and x2 +y2 = 4 . The value of the integral
JJsin (x2 +y2)dx dy
is
(A) (cos 1 - cos 2) 4
(B) (cos 1-cos 4) 4
(C) (cos 1-cos 2)
(D) (cos 1-cos 4)
2 f(x, y) = (x + yf - (x + y) +1.
The absolute maximum value and the absolute minimum value of the function on the unit square {(x, 3/) : 0 < x < 1, 0 < y < l}, respectively are
(A) 3 and -
(B) and
2 4
(C) 3 and -
4
(D) 2 and -
4
11. For A > 0, the value of the integral
je-Ax2dx
0
|
equals |
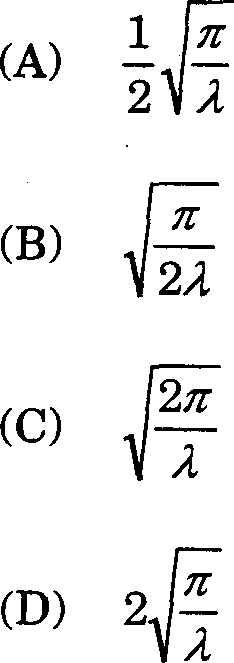 |
. (x' = x sin I
Vy.
-\,xy*0. x
+ y sin
Then x+y~ is equal to dx J dy H
(A) -z
(B) 0
(C) 2
(D) 2z
13. Let
f(x) = x3-x2 +1, 0<ac<l.
Then the absolute minimum value of f(x) is 14
(A)
27
9
23
(C)
27
(D) 1
14. The slope of the tangent line to the curve
x=a(t-sini), y = a(l-cosi), te R,
tr * n
at t = is
(A) -1
(B) 0
(C) 1
(D) oo
15. Consider the equations
sin(cosx) = x (1)
and
cos(sinx) = -x (2)
for x > 0. Then
(A) Only Equation (1) has a solution
(B) Only Equation (2) has a solution
(C) Both Equations (1) and (2) have solutions
(D) Neither Equation (1) nor Equation (2) has a solution
16. If
- a+h
lim [ e dt = 1, h. j
h-*o h
a
then the value of a is
(A) -1
(B) 0
(C) 1
(D) 2
17. Let
fix, y) = x3 +;y3 +3x2 -3y2 -5.
Then the local maximum and the local minimum of the function f are at the points
(A) (-2,0) and (-2, 2), respectively
(B) (-2, 0) and (0, 2), respectively
(C) (0, 2) and (-2, 0), respectively
(D) (0, 2) and (0, 0), respectively
18. Let 9, 0 < 6 < n be the angle between the planes x - y + z = 3 and 2x-z = 4.
The value of 6 is '1'
-l
(A) cos
(B) cos-1
(C) cos-1
(D) cos-1
' 1 N <Vl5 j
' 3 ' ,Vl5,
19. Let
f(x, y) = xy2 +yx2.
Suppose the directional derivative of fin the direction of the unit vector (u1} (l, -l) is 1. Then among the following, (u, u2) is
u2) at the point
(A) (-1,0)
(B) (0,1)
(C) (1,0)
(D)
20. The point on the sphere x2 +y2 +z2 =1 farthest from the point (l, -2, l) is
'zl JL zl V V V
(A)
(B)
(C)
(D)
V V V.
-1 _2_ J_
VVV.
/ 1 2 -1 VeVV
21. Consider the dihedral group Z)4 = {e, r, r2,r3, f, rf, r2f, r3f} with r4 = e-f2 and rf = fr~ The product rzfr~1f~lr3fr corresponds to
|
(A) |
f |
|
(B) |
rf |
|
(C) |
r2f |
|
(D) |
r3f |
|
Let p |
and q be distinct |
|
Suppose S = H n{p,q, | |
|
(A) |
\pQ,Pq,QP} |
|
(B) |
{p + , PQ,P9} |
|
(C) |
(p,pq, P9) |
|
(D) |
{p,p + q, pq} |
23. The number of group homomorphisms from the group ( Z18, 18) to the group (Z30, 30 ) is
(A) 3
(B) 4
(C) 5
(D) 6
24. Let <7 = (125) (36) and z = (1456) (23) be two elements of the permutation group on 6 symbols. Then the product a, where crr(i) = cr(r(i)), is
(A) (14) (26) (35)
(B) (13) (26) (45)
(C) (14) (25) (36)
(D) (13) (24) (56)
25. Let G = {ns 1 < /z < 55, gcd (n, 56) = 1} be a multiplicative group modulo 56. Consider the sets
Sj = {1, 9,17, 25, 33, 41} and S2 = {l, 15, 29, 43}.
Which one of the following is TRUE?
(A) Sx is a subgroup of G but S2 is NOT a subgroup of G
(B) is NOT a subgroup of G but S2 is a subgroup of G
(C) Both S1 and S2 are subgroups of G
(D) Neither S1 nor S2 is a subgroup of G
26. Let G be a group with respect to multiplication. If x = a42 + /?V3 g G then x 1 is ot42+/?V3
(A)
(C)
|
(B) |
| ||||||||||||
|
(D) 2a2 + 3/?2 | |||||||||||||
27. Let G = {l, 2, , p -1} be the group with respect to multiplication modulo p. If the inverse of 110 in G is 4, then p is of the form
(A) 5n + 1
(B) 5n + 2
28. Consider the alternating group Ai = {ctg S4 : a is an even permutation}. Which of the following is FALSE?
(A) A4 has 12 elements
(B) A4 has exactly one subgroup of order 4
(C) A4 has a subgroup of order 6
(D) Number of 3 cycles in A4 is 8
29. Let P be a 3x3 matrix such that for some c, the linear system Px = c has infinite number of solutions. Which one of the following is TRUE?
(A) The linear system Px = b has infinite number of solutions for all b
(B) Rank (P) = 3
(C) Rank(P)*l
(D) Rank (P)< 2
30. Let
/(jc) = jc3 +x2 -x+15 and g(x) = x3 + 2x2 -x + 15 .
Then, over Q
(A) /"is irreducible and g is reducible
(B) f is reducible and g is irreducible
(C) Both f and g are reducible
(D) Both f and g are irreducible
31. Let
|
'I |
a |
O' |
r r |
* |
fa |
0 |
0N |
rr | ||||||
|
< |
0 |
1 |
0 |
i |
ae R |
and V = |
0 |
a |
0 |
l |
:ae R | |||
|
,0 |
0 |
1, |
,oJ |
0 |
K |
The angle between U and V is
(A) 0
4
P =
,1 3 1 Then 8P_1 is equal to
v
/
|
' 13 |
-4 |
-i\ | |
|
(A) |
-15 |
4 |
3 |
|
,io |
0 |
-2, | |
|
'13 |
-15 |
10'N | |
|
(B) |
-4 |
4 |
0 |
|
l-l |
3 |
-2, | |
|
"13 |
10 |
-151 | |
|
(C) |
-4 |
0 |
4 |
|
l-l |
-2 |
3 , | |
|
M CO |
-4 |
-1! | |
|
(D) |
10 |
0 |
-2 |
|
1-15 |
4 |
3, |
33. Let P be an n xn idempotent matrix, that is, P2 = P. Which of the following is FALSE?
(A) PT is idempotent
(B) The possible eigenvalues of P are 0 or 1
(C) The nondiagonal entries of P can be zero
(D) There are infinite number of n x n nonsingular matrices that are idempotent
34. Let V be the vector space of all polynomials with real coefficients. If W is the vector subspace of V generated by
1-x, x2 -x, x2 -1 and x2 -3x+ 2,
then the dimension of W is
(A) 1
(B) 2
(C) 3
(D) 4
35. Let
P =
Then
(A) P has two linearly independent eigenvectors
(B) P has an eigenvector
(C) P is nonsingular
(D) There exists a nonsingular matrix S such that S_1PS is a diagonal matrix
36. Let u, ve R3, v * 0. Which of the following is FALSE?
is the length of the projection of u along v
(A)
u
(B) If u w = v w for all w e R3, then u = v
(D) | a + v f +1| u - v f = 2 (HI2 + M2)
37. Let P be a 2x2 matrix such that P102 = 0. Then
(A) P2 = 0
(B) (J-P)2=0
(C) (/ + P)2=0
(D) P = 0
38. Let
P =
-i
The eigenvectors corresponding to the eigenvalues i and - i are respectively
(B) (C) (D) (A)
39. The area of the parallelogram with sides x = i + j+k and y = - i + j is (A) & (B) 2V3 (C) 3V2 (D) 6 > > x=i + ./+ &, y = ai + k and z = i + aj . Then the volume of the parallelopiped with sides x, y and z is (A) 1 + a+a2 (B) 1 + a-a2 (C) 1-a + a2 (D) a2+a-l 41. The solution of the initial value problem xy'-y = 0 with y( 1) = 1 is (A) y{x) = x 1 (B) y{x) = - x (C) y(x) = 2x -1 2x -1 42. Let y(x) = xsinx be one of the solution of an nth order linear differential equation with constant coefficients. Then the minimum value of n is (A) 1 (B) 2 (C) 3 (D) 4 fxz \ --hx + siny dy = 0 (x2y + xy2)dx + 3 is X3v X2V2 (A) + cos y = c 3 2 J 3 2 2 /r\ x y x y (B) - +----h COS y - C 3 2 x3 xV (O cosy = c 3 6 X3 x2v3 (D) + + cosy=c 3 6 J 44. The general solution of the differential equation /// rr / a is (A) +xc2 + x2c3)e* (B) ip1+xc2+x2ca)e~x (C) c1ex +(c2 + xc3)e~x (D) (cj +xc2)c* + c3ex 45. Let f(x) = 2x3 -x2 +2x-5 . Consider the following statements about the roots of f(x) = 0 P : At least one root is positive. Q : At least one root is negative. R : There is a root between x = 1 and x = 2. Which one of the following is TRUE? (A) P, Q and R are valid statements (B) P and Q are valid statements but R is NOT a valid statement (C) P and R are valid statements but Q is NOT a valid statement (D) P is a valid statement but Q and R are NOT valid statements 46. The maximum absolute error that occurs in rounding off a number after 6 places of decimal is (A) 5xl0-8 (B) 1(T7 (C) 5xlCT7 (D) 5x10" 47. Which of the following is FALSE? (A) A unique interpolating polynomial of degree n is obtained from the given values at fixed n +1 points (B) The Lagrange interpolation formula can be applied to equispaced points (C) The Newtons forward difference interpolation formula can be applied to non-equispaced points (D) The trapezoidal rule gives exact value of the integral for linear functions
Applying Simpsons one third rule, the value of the integral 3 jY(.x) dx is (A) 10 (B) 12 (D) 15 49. Consider f(x) = l + xe~x. The Newton-Raphson iterative scheme for finding a root of f(x) = 0 is (xn -l)e* _ x\ e~x" +x(L + e~*-)-l l + xe n (C) r _x2ne~x* +xn(l-e-x')+l vW xn+l --: l + xe " 50. Consider the following Primal Linear Programming Problem : Maximize cTx Subject to JPx = b x>0 The Dual Linear Programming Problem is (A) Minimize yTb Subject to : PTy = c, y unrestricted (B) Minimize yTb Subject to : PTy>c, y unrestricted (C) Minimize yTb Subject to : PTy = c, y>0 (D) Minimize yTb Subject to : PTy>c, y>0 51. If the Primal Linear Programming Problem is unbounded then which of the following is TRUE? (A) Dual problem is unbounded (B) Dual problem has a single bounded optimal solution (C) Dual problem has multiple bounded optimal solutions (D) Dual problem is infeasible 52. Which of the following pair of linear programming constraints is equivalent to the inequality | xx - x2\ a ? (A) x1-x2 <a, x2-x1 <a (C) x1-x2<-a, x2-x1<-a (D) x1-x2 < -a, x2-x1<a 53. Consider the following Linear Programming Problem : Maximize 3xj + 8x2 Subject to 2xx +5x2 <10 6! + x2 6 xlt x2>0 The optimal value of the objective function is
54. A cow is tied with a pole by a 100 meter long rope. What is the probability that at some point of time the cow is at least 60 meters away from the pole? q (A) 25 25 (C) 25 18 (D) 25 55. Two letters are chosen one after another without replacement from the English alphabet. What is the probability that the second letter chosen is a vowel? (A) -z~ (B) (C) (D) 4_ 25 5_ 26 _5_ 25 1 _1_ 5 26 56. Let X be a binomial random variable with parameters n and p. If the mean and the standard deviation ofX are 3 and , respectively, then what is the value of (n, p)? (A) |4,J (C) 9, - / (D) 57. Let X,Y,Z be independent Poisson variables, such that E(X) = E(Y) and E(Z) = 2E(X). If P{X = 5, Y = 4) is equal to P(Z = 8), then E (X) is 2 21 7 21 7 21 21 (A) (B) (C) (D) 58. The largest natural number whose base 7 representation has exactly four digits, is (A) 2400 (B) 6666 (C) 7777 (D) 2401 59. 10s complement of the decimal number 56789 is (A) 01234 (B) 12345 (C) 43210 (D) 43211 60. Let x = 0.125E + 01, y = (l.0l)2 and z = (l.2)g . Which of the following is TRUE? (A) x, y and z are equal (B) Only x and y are equal (C) Only x and z are equal (D) All x, y and z are different 61. The decimal value of (2l)8 x(l0l)16 lies in the interval (A) 3000 - 3499 (B) 3500 - 3999 (C) 4000 - 4499 (D) 4500 - 4999 62. The binary equivalent of the hexadecimal number A52C is (A) 1010101101100 (B) 1010010100101100 (C) 1010111000101100 (D) 1010010100101101 63. Let x, y and z be Boolean variables. The number of possible values for the expression xy + zx is (A) 1 (B) 2 (C) 4 (D) 8 64. Let x and y be independent Boolean variables, each taking values 0 or 1 with probabilities- 0.5 and 0.5, respectively. The probability that x + y(x+y) = 1
.s 65. The Boolean expression (x + y)(y + z)(z+x)
66. Let X and Y be 4 bit registers with initial contents as 1011 and 1001, respectively. The following sequence of operations are performed on the two registers : Y<r-XY X<XY Y<r-XY where denotes XOR operation. The final contents of the two registers are (A) X =1001, Y = 1011 (B) X =1011, Y= 1001 (C) X = 1011, Y= 1011 (D) X =1001, Y = 1001 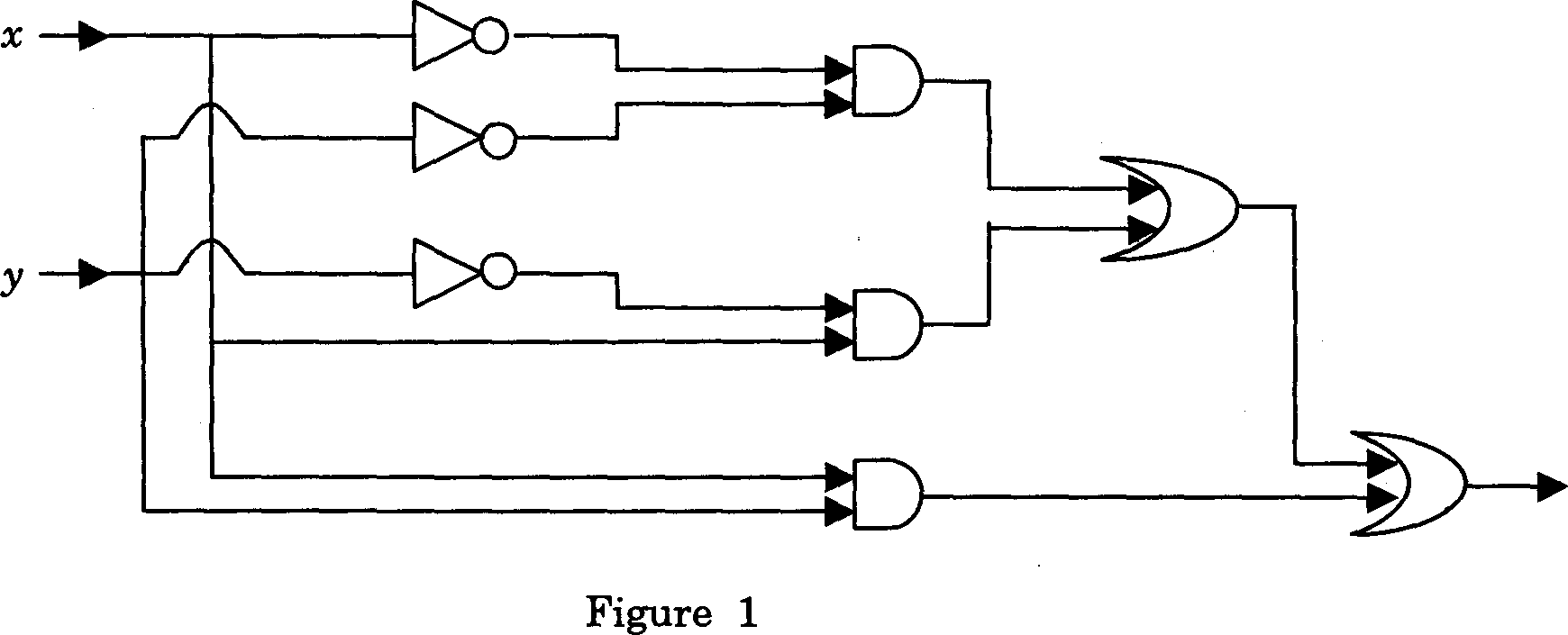
The logic circuit diagram shown in Figure 1 is equivalent to the Boolean expression (A) x + y (B) x + y (C) x+y (D) x+y
The logic circuit diagram given in Figure 2 is equivalent to ->\>o 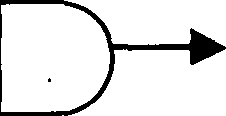 (A) AND gate (B) OR gate (C) NAND gate (D) XOR gate 69. BIOS is the acronym for (A) Binary Input Output Source (B) Basic Input Output Support (C) Binary Input Output System (D) Basic Input Output System 70. The maximum number of characters that can be encoded in a fixed length encoding sehen with n bits is (A) 2" (B) n! (C) n2 (D) n 71. Which of the following is an 8-bit processor? (A) Intel 80286 (B) Intel 8086 (C) Intel 8085 (D) Intel Pentium II 72. For which of the following combinations an SR Flip-Flop is set to 1? (A) S = 0, R = 0 (B) S = 0, R = 1 (C) S = 1, R = 0 (D) S = 1, R = 1 73. For which of the following combinations, a JK Flip-Flop will enter into the complement of the present state? (A) J = 0, K = 0 (B) J = 0, K = 1 (C) J = 1, K = 0 (D) J = 1, K = 1 74. Which of the following is NOT a Software? (A) Adobe (B) Browser (C) Compiler (D) Device Driver List 1 1. Operating Systems P. Pentium Q. Linux R. Router S. Anti Virus 2. Application Software 3. Processor 4. Network (A) (1, Q), (2, S), (3, P), (4, R) (B) (1, Q), (2, R), (3, P), (4, S) (C) (1, P), (2, S), (3, Q), (4, R) (D) (1, P), (2, R), (3, S), (4, Q) 76. Match the file extensions in List 1 with the corresponding applications in List 2
(A) (1, Q), (2, S), (3, R), (4, P) (B) (1, Q), (2, S), (3, P), (4, R) (C) (1, Q), (2, P), (3, S), (4, R) (D) (1, Q), (2, R), (3, P), (4, S) (A) Magnetic Tape (B) Hard Disk (C) Floppy Disk (D) CD 78. Which of the following is a valid C directive? (A) # include <stdio.h>; (B) # include <stdio.h> (C) include <stdio.h>; (D) include <stdio.h> 79. Consider the following declaration in C struct student { char name [12] ; float gradepoint ; struct student MCA [5] ; The number of bytes needed to store the array MCA is (A) 16 (B) 25 (C) 70 (D) 80 80. Consider the following C statements P : for (i = 0; i < 8; i+ = 3) {printf ("*");} Q : for (i = 4; i > 0; i- = 2) {printf ("*");} R : for (i = 0; i <= 9; i+ = 3) {printf ("*");} S : for (i = 0; i < 7; i + +) {if (i %3 = = 0) printf ("*");} Which one of the following is a TRUE statement? (A) P, Q, R and S give the same output (B) P and S give the same output (C) Q and R give the same output (D) P, Q and S give the same output 81. Consider the following program segment {intx, i, j ; x = 0; for (t = 0; i < 19; i + +) for (j = i + l; j < 20; j + +) * ++;} The value of x after executing the segment is (A) 171 (B) 190 (C) 342 (D) 380 82. Let f: N> N be defined as w \ _ f 1> if n = 1 or n = 2 \f(n -1) + f (n - 2), otherwise. What is the value of /"(IO) ? (A) 34 (B) 45 (C) 55 (D) 89 83. Consider the following program segment {int n = 1; float x, term-, float sum = 1; term = 1; while (n < 51) { term * = -x*x/(n*(n +1)); sum + = term ; n + = 2; } } For a given x the value of sum approximates the function (A) sin* (B) cosac (C) e-1 (D) e*2 84. Consider the following program void swap (int a, int b) {int temp ; temp = a ; a = b ; b =a ; } void main () {int x, y; x = 2; y = 3; swap (x,y); printf ("re = %d y = %d \n", x, y); } The output of the program is (A) x = 2 y-2 (B) x = 2 y = 3 (C) x = 3 y = 2 (D) x = 3 y = 3 85. What is the output of the following C program? void fun (int * p) {int i, sum = 0 ; for (i = 2; <4; ++ i) sum + = * (p + i); printf ("%d", sum); } void main () {int a[ 5 ] = {10, 20, 30, 40, 50}; fun (a +1); }
86. Consider the following C program segment int gradepoint ; char ch; switch (ch) { case A : {gradepoint = 10 ;} case B : {gradepoint = 8 ; break ; } case C : {gradepoint = 6 ; } default : {gradepoint = 0 ;}} Executing the program segment for ch = A, B\ C gradepoints are respectively (A) 10, 8, 6 (B) 10, 8, 0 (C) 8, 8, 6 (D) 8, 8, 0 87. Consider the following C program void main () { int i, s ; for (i = 0;; i + +) {s = s + i / (i-2); if (i > 5) break; } } Which one of the following is a TRUE statement? (A) There is a syntax error (B) There is a type mismatch error (C) There is a runtime error (D) There is no runtime error 88. The unit place of the number 2782 is (A) 1 (B) 3 (C) 7 (D) 9 89. The number of all functions is (A) m(m-l)-(m-n+l) (B) n (re-l)-- (/i-m+l) (C) mn (D) nm 90. The number of ways in which 4 boys and 5 girls can sit in a row so that there is a girl between any two boys is (A) 4! 5! (B) 3 (4! 5!) (C) 5 (4! 5!) (D) 15 (4! 5!) ' 91. The next term in the series 191, 211, 232, 254, is (A) 267 (B) 276 (C) 277 (D) 287 92. If sinx+cosx= then sin(2x) is (A) 1 -a2 (B) a2 -1 (C) 1+a2 (D) a2 93. A student computes the sum of squares of the first 40 natural numbers and gives j incorrect answer 22019. By mistake, the student forgot to add the square of one of t numbers. The missed number is (A) 5 (B) 7 (C) 9 (D) 11 94. For a,be Z, define a relation aRb if ab > 0. Then the relation R is (A) symmetric, reflexive and transitive (B) symmetric and reflexive but NOT transitive (C) symmetric and transitive but NOT reflexive (D) reflexive and transitive but NOT symmetric 95. What is the sum of the interior angles of an n vertex simple polygon? (A) {n-2)n (B) (C) ln+1- 96. Who among the following is NOT a Nobel Laureate? (A) Amartya Sen (B) J.C. Bose (C) Muhammad Yunus (D) S. Chandrasekhar 97. Who is the father of Bhishma in the Mahabharata? (A) Bharat (B) Devavrata (C) Parashar (D) Shantanu 98. Which country won the 2006 FIFA World Cup? (A) Argentina (B) France (C) Germany (D) Italy 99. Which of the following diseases is NOT caused by mosquito bite? (A) Dengue (B) Encephalitis (C) Malaria (D) Typhoid is (A) 2-V2 (B) 3-V2 (C) 2W2 (D) 3+V2 2 +- 2 + 2+-. 2 +- l + xe n
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
