Anna University Coimbatore 2008 B.E Electrical and Electronics Engineering Numerical methods Model - Question Paper

MODEL EXAMINATION

 

NUMERICAL METHODS

 

Year/Branch/Sem : II / EEE / IV Marks: 100

 

PART-A (20X2=40)

1. Solve 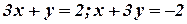by Gauss-Seidal iteration method.
2. Give an example of (a) algebraic (b) transcendental equation.
3. Find the inverse by Gauss-jordan method.
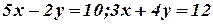4. What are the 2 types of errors involved in the numerical computation?
5. State Gregory-Newton backward difference interpolation formula.
6. State the order of convergence of cubic spline.
7. State Lagranges interpolation formula.
8. Find the divided difference table for the following data

x : 2 5 10

y : 5 29 109

9.     By differentiating Newtons backward formula, find the first derivative of the function f(x).

10.                        Evaluate 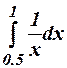by Trapezoidal rule , dividing the range into 4 equal parts .

11.                        Six sets of values of x and y are given (xs being equally spaced).

Write the formula to get .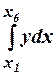

12.                        Write down the trapezoidal rule to evaluate 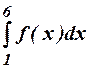with h=0.5 .

13.                        Solve the differential equation by Taylor series method to get the value of y at x=h.

14.                        Write down the Runge-Kutta formula of fourth order to solve

15.                        How many prior values are required to predict the next value in Adams method?

16.                        State the special advantage of Runge-Kutta method over Taylor series method.

17.                        Write down the Crank-Nicolson formula to solve .

18.                        Write the diagonal five point formula to solve the Laplacian equation.

19.                        What is the classification of one dimensional heat flow equation?

20.                        Write an explicit formula to solve numerically the heat equation (parabolic equation) .

 

PART-B ( Answer any 5 ) 5 X 12 = 60

21.                        a) Using Newtons iterative method , find the root between 0 & 1 of

correct to 6 decimal places.

b) Find a real root of the equation by iteration

method.

22.                        Solve the following system by Gauss-Seidal method

.

23.                        a) Using Lagranges interpolation formula find y(10) given that

y(5)=12,y(6)=13,y(9)=14,y(11)=16.

b) Using Newtons divided difference formula, find u(3) given

u(1)=-26,u(2)=12,u(4)=256,u(6)=844.

24.                        Using Newtons forward interpolation formula, find the polynomial f(x) satisfying the following data. Hence evaluate y at x=5.

x:	4	6	8	10
y:	1	3	8	10

25.                        Dividing the range into 10 equal parts , find the value of 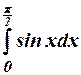by (i) Trapezoidal rule (ii) Simpsons rule.

26.                        a) Evaluate 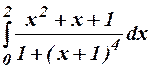by Gaussian three point formula.

b)    Solve by Taylors series method. Find the

values y at x=0.1 and x=0.2.

27.                        a) Using Eulers method find y(0.3) of y(x) satisfies the initial value

problem.

b)Using R.K. method of 4^th order, solve 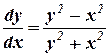with y(0) =1

at x=0.2.

28.                        Approximate the solution to the wave equation withfor 3 time steps .