Anna University Coimbatore 2008 B.E Transforms and Partial Differential Equation - Model - Question Paper
Wednesday, 16 January 2013 07:15Web
MODEL EXAMINATION
TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATION
Year/Semester & Branch: II / III Common to all Branches
Max. Marks: 100 Time: 180 min
PART-A Answer ALL Questions (20X2=40)
- If
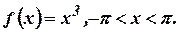 Find
constant term
Find
constant term 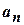 of its
Fourier series.(Tri-N/D 08)
of its
Fourier series.(Tri-N/D 08) - Find the root mean square value of
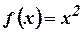 in the interval
in the interval 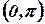 . (A/M 08)
. (A/M 08) - State Dirichlets condition for Fourier series. (Tnl-N/D 08) (Nov 05)
- The Fourier series expansion of
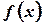 in
in 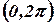 is
is 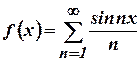 . Find the root
mean square value of
. Find the root
mean square value of 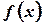 in
the interval
in
the interval 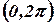 .
(Cbe-N/D 08)
.
(Cbe-N/D 08) - State the Convolution theorem of the Fourier transform. (A/M 08)
- State Fourier integral theorem. (A/M 08) (Cbe-N/D 08)
- Write the Fourier transform pair (N/D 07).
- Find the Fourier sine transform of
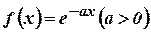 . (N/D 07).
. (N/D 07). - Find the complete integral of
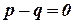 (Cbe-N/D 08)
(Cbe-N/D 08) - Form a partial differential equation by eliminating
arbitrary constants a and b from
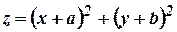 . (A/M 08)
. (A/M 08) - Solve
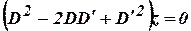 (A/M
08).
(A/M
08). - write the complete integral of
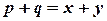 . . (Tnl-N/D 08)
. . (Tnl-N/D 08) - Classify the differential equation
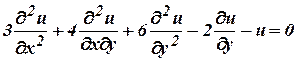 (Cbe-N/D 08)
(Cbe-N/D 08) - The ends A and B of a rod of length 10cm long have their
temperature kept at
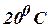 and
and
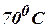 . Find the
steady state temperature distribution of the rod. (A/M 08)
. Find the
steady state temperature distribution of the rod. (A/M 08) - Find the steady state temperature distribution in a rod of
length 10cm whose ends x=0 and x=10 are kept at
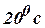 and
and 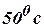 respectively.
(Tri-N/D 08)
respectively.
(Tri-N/D 08) - Write the initial conditions of the wave equation if the string has an initial displacement but no initial velocity. . (Tnl-N/D 08)
- Form a difference equation by eliminating arbitrary
constants from
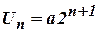 .(Cbe-N/D
08)
.(Cbe-N/D
08) - Define Z-transform of the sequence
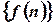 (Cbe-N/D 08)
(Cbe-N/D 08) - If
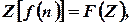 What
is
What
is 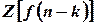 ? (Tri-N/D 08)
? (Tri-N/D 08) - Prove that
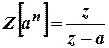 .
(Apr/May 1999), (Apr/May 2000)
.
(Apr/May 1999), (Apr/May 2000)
PART-B (Answer ANY 5 questions) (5 X 12 = 60)
- a)
Obtain Fourier cosine series for
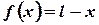 in
in 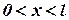 .(Tri-N/D
08)
.(Tri-N/D
08)
b) Compute the first two harmonics of the
Fourier series of ![]() given in
given in
the following table:
x : 0 ![]()
![]()
![]()
![]()
![]()
![]()
![]() : 1.0 1.4
1.9 1.7 1.5 1.2 1.0 (A/M 08)
: 1.0 1.4
1.9 1.7 1.5 1.2 1.0 (A/M 08)
- Find
the Fourier transform of
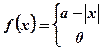

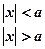 . Hence show that
. Hence show that
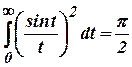 and
and 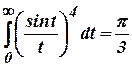 (Cbe- N/D
08)
(Cbe- N/D
08) - a) Solve
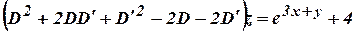 (Cbe-
N/D 08)
(Cbe-
N/D 08)
b) Solve ![]() (Cbe- N/D 08)
(Cbe- N/D 08)
- A rectangular plate with insulated surface is 10 cm wide
and so long compared to its width that it may be considered infinite in
length without introducing appreciable error. The temperature at short
edge y=0 is given by
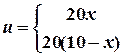
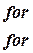
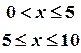 and all the
other three edges are kept at
and all the
other three edges are kept at 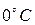 .
Find the steady state temperature at any point in the plate. (A/M
08)
.
Find the steady state temperature at any point in the plate. (A/M
08) - a) Find the Z-transform of
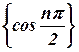 and
and 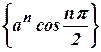 (Cbe- N/D 08)
(Cbe- N/D 08)
b) Find the inverse Z-transform
of 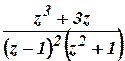 (Cbe- N/D 08)
(Cbe- N/D 08)
- a) Find the Fourier sine series for
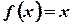 in
in 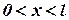 (Tri-N/D 08)
(Tri-N/D 08)
b) Find the Fourier transform of 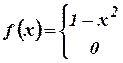
![]()
![]() (Tri-N/D 08)
(Tri-N/D 08)
- A string is stretched and fastened to two points l
apart. Motion is started by displacing the string into the form of the
curve
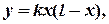 and then
releasing it from this position at time t=0. Find the displacement
of the point of the string at a distance x from one end at time
t . (A.U.Tri. Nov/Dec 2008) (Dec 2008) (May/June 2009)
and then
releasing it from this position at time t=0. Find the displacement
of the point of the string at a distance x from one end at time
t . (A.U.Tri. Nov/Dec 2008) (Dec 2008) (May/June 2009) - a) Solve
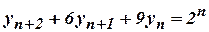 given
given
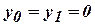 , using
Z-transform (Tnl-N/D 08)
, using
Z-transform (Tnl-N/D 08)
b) Solve 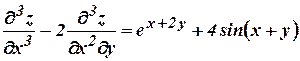 (A/M 08)
(A/M 08)
| Earning: Approval pending. |
