Anna University Coimbatore 2009 B.E Transforms and Partial Differential Equation - Model - Question Paper
MODEL EXAMINATION
TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATION
Year/Semester & Branch: II / III Common to all Branches
Max. Marks: 100 Time: 180 min
PART-A Answer ALL Questions (20X2=40)
1. Determine
the value of 
in the
Fourier series expansion of 
.
(A/M 08)
2. Define
Root mean square of over the range 
.
(Tri-N/D 08)
3. If 
in the interval
(0,4), then find the value of 
in
the Fourier series expansion. (Cbe-N/D 08)
- State Dirichlets condition for Fourier series. (Tnl-N/D 08) (Nov 05)
- Let
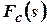be
the Fourier cosine transform of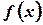 
.
Prove that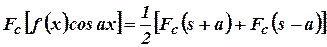 
.
(Cbe-N/D 08) - State Fourier integral theorem. (A/M 08) (Cbe-N/D 08)
- If
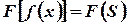then
prove that 
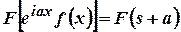(Tnl-N/D
08) - what is the sine transform of
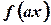if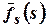 
is the Fourier
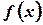sine transform of .(Tri-N/D
08) - Form the partial differential equation by eliminating arbitrary
constants from
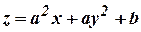(Cbe-N/D
08) - Find the complete integral of
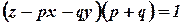(N/D 08). - Eliminate the function f from
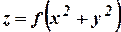(Tnl-N/D 08). - Write the complete integral of
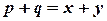(Tnl-N/D 08) - A rod 50cm long with insulated sides has its ends A and B
kept at
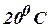and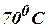 
respectively.
Find the steady state temperature distribution of the rod. (Cbe-N/D 08) - Classify the partial differential equation
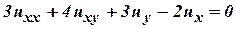. (A/M 08) - Write the initial conditions of the wave equation if the string has an initial displacement but no initial velocity. (Tnl-N/D 08)
- List all the possible solutions of the one dimensional wave equation and state the proper solution. (Tri-N/D 08)
- Form the difference equation from
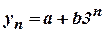. (A/M 08) - Find
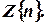(A/M
08) (Tnl-N/D 08) - If
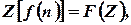What
is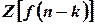 
? (Tri-N/D 08) - Find the Z- transform of
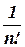. (Tri-N/D 08)
PART-B (Answer ANY 5 questions) (5 X 12 = 60)
- a) Obtain the Fourier series of
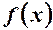of period 2l
and defined as follows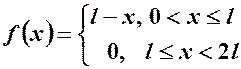 
.Hence
deduce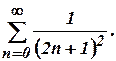
(Tnl-N/D 08)
b) Find the half range sine
series of 
in 
(Tnl-N/D 08)
- Find the Fourier cosine transform of
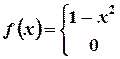
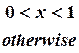. Hence prove
that 
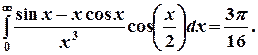(Tnl-N/D
08) - a) Solve
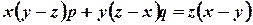.(Tri-N/D
08)
b) Solve 
.(Tri-N/D 08)
- If a string of length l is initially at rest in
its equilibrium position and each of its points is given a velocity v
such that
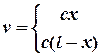
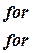
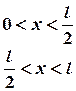. Determine the
displacement function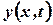 
at
any time t.(Cbe N/D 08) - a) Find the Z-transform of
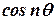and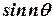 
. Hence find 
.
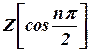b) Solve 
using Z-transform
given 
.
- a) Obtain the Fourier series upto second harmonic from the data
x : 0 
: 0.8 0.6 0.4
0.7 0.9 1.1 0.8 (Cbe N/D 08)
b) Find the Fourier cosine
transform of 
. Hence deduce the
value of
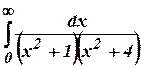.(Tri-N/D 08)
- The ends A and B of a rod l cm long have their
temperatures kept at
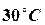and
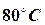, until steady
state conditions prevail. The temperature at the end B is suddenly
reduced to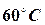 
and
that of A is increased to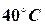 
.Find
temperature distribution in the rod after timet.(Tnl-N/D 08)
- a) Find
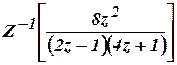using
Convolution theorem. (Tnl-N/D 08)
b) Find the singular integral of 
. (Cbe N/D 08)
| Earning: Approval pending. |
