Anna University Coimbatore 2008 B.E Computer Science and Engineering Discrete Mathematics Model - Question Paper
MODEL EXAMINATION
DISCRETE MATHEMATICS
Year/Branch/Sem : II /IT , CSE / IV Marks: 100
Time:9.10-12.10
PART-A (20 X 2 = 40)
1. Write the dual of (a)
(b)
(c) 
.
2. Show that 
.
3. Represent 
using 
only.
4. Determine the truth value of the following a) If 3+4=12 , then 3+2=6.
b) If 3+3=6 , then 3+4=9.
5. Find the truth value
of 
where
.
6. Prove that 
.
7. If the universe of
discourse is the set 
eliminate the
quantifiers in the formula
.
8. Give the symbolic form of the statement
Every book with a blue cover is a Mathematics book.
9. For any sets A , B and C
, Prove that 
.
10. Define Characteristic function.
11. Define Partially ordered set.
12. Give an example of a relation which is both reflexive and
symmetric.
13. If 
denotes the
characteristic function of the set 
.Prove
that 
for all 
.
14. If has 3 elements and 
has 2 elements. How many
functions are there from to .
15. Define odd and even permutation.
16. Define Partially ordered set.
17. Let 
and 
where 
is the set of real
numbers. Find 
where 
.
18. A semi group homomorphism preserves property of associativity
19. Find all the cosets of the subgroup 
in 
with the operation
multiplication.
20. Define ring and give an example of a ring with zero-divisors.
PART-B (Answer any 5) (5 X 12 =60 )
21. Without using truth tables & also use truth tables,Obtain PDNF
& PCNF of 
.
22. a) Show that the following premises are inconsistent:
1. If Jack misses many classes through illness and reads a lot of
books.
2. If Jack fails high school, then he is uneducated.
3. If Jack reads a lot of books, then he is not uneducated.
4. Jack misses many classes through illness & reads a lot of
book
b) Using Indirect method of proof , show that
23. a) Prove that
.
b) Show that
24. a)Show that if L is a
distributive lattice then for all 
.
b)Establish De Morgans laws in a Boolean algebra.
25. a)Let R denote a relation on the set of ordered pairs of positive
integers such that 
iff
. Show that R is
an
equivalence relation.
b)Prove that any chain a is modular lattice.
26. a)If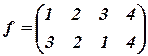 
& 
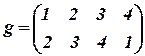are
permutations, prove that 
.
b)
Let the function 
and 
be defined 
and
.Determine the
composition function 
and 
.
27. a). Find all the mappings from 
to 
find
which
of them are 
and which are onto.
b) Find the minimum distance of the encoding function
given
by
.
28. a)State & prove Lagranges theorem for finite groups.
b) Show that 
encoding function
defined by
is
a group code.
| Earning: Approval pending. |
