Anna University Coimbatore 2009 B.E 2 ks with Answer for Transforms and Partial Differential Equations ( Unit-3 PDE) - Question Paper
TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS
ANNA UNIVERSITY (2 Marks) QUESTIONS WITH ANSWERS
UNIT III
PARTIAL DIFFERENTIAL EQUATIONS
TWO MARKS
1)
Solve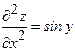 
.
Solution:
2)
Find the complete
integral of 
.
Solution:
Given, 
This
is of the form 
Hence the
Complete integral is 
3)
Form the PDE by
eliminating the arbitrary constants a and b from the equation 
.
Solution:
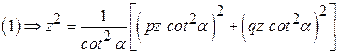
4)
Find the complete
solution of the PDE 
.
Solution:
Given, 
The
complete integral is 
Hence
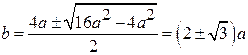
Therefore,The
complete solution is 
5) Form the PDE of all spheres whose centers lie on the z-axis.
Solution:
The equation of such spheres with centre (0,0,c) and radius r is
where
r, c are constants.
Differentiating
p. w.r.to x and y , we get
Substituting
(3) in (2), we get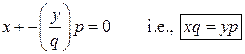 
6)
Find complete
integral of the PDE 
.
Solution:
Given, 
This is of the form 
.
The Auxillary equation is 
Now Consider 
Integrating this we get 
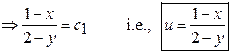
Now Consider 
Integrating this we get 
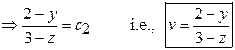
Hence, The General Solution is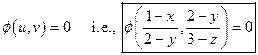 
7)
Obtain the PDE by
eliminating the arbitrary constants a and b from the equation 
.
Solution:
,
Similarly,
8)
Find the general
solution of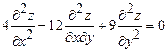 
.
Solution:
The Auxillary equation is
9)
Eliminate the
arbitrary function f from 
and
form the PDE.
Solution:
Differentiating the given equation p.w.r.to 
and
,
Divide
by
.
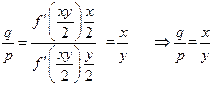10)
Find the Complete
integral of 
.
Solution:
Given 
This
is of the form 
Solution is 
subject
to
.
This is the C.I. of 
11) Find the PDE of all planes passing through the origin.
Solution:
The general equation to a plane is 
where a, b, c, d are constants.
Since 
passes
through 
Substitute
the values of a & b in 
.
12)
Find the
particular integral of 
.
Solution:
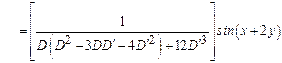
13)
Find the solution
of 
.
Solution:
Given, 
This
is of the form 
.
The Auxillary equation is
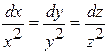
Now
Consider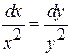 
Integrating
this we get 
Now
Consider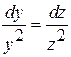 
Integrating
this we get 
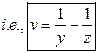
Hence, The
General Solution is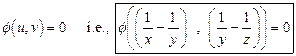 
14)
Solve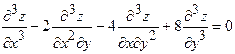 
.
Solution:
satisfies
this equation , 
also
satisfies this equation and 
The
roots are 
Solution
is 
where
are
arbitrary functions of 
.
15)
Solve 
.
Solution:
Solution
is 
where
are
arbitrary functions of 
.
16)
Form the PDE by
eliminating the arbitrary constants a and b from 
.
Solution:
Differentiating the given equation p.w.r.to and
,
Substituting
&
in
,
.
17)
Solve 
Solution:
The given equation can be written as 
The
complete solution is 
.
18)
Solve 
Solution:
.
Solution
is 
.
19)
Form the PDE by
eliminating the arbitrary function from 
.
Solution:
Differentiating 
p.w.r.to
in
turn,
Equating
&
we
get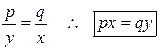 
20)
Write down the
complete solution of 
.
Solution:
The given PDE is
Clairauts Form 
The complete solution is got by putting 
in
the given PDE.
The
C.I. is 
where
and
are
arbitrary constants.
21)
Find the singular
solution of 
.
Solution:
This is Clairauts Form. Hence the complete integral
is 
Differentiating
partially
w.r.to and
respectively
we get
and
Substituting
in we
get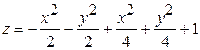 
.
22)
Find the general
solution of 
.
Solution:
Given, 
This
is of the form 
.
The
Auxillary equation is 
Now
Consider 
Integrating
this we get 
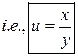
Now
Consider 
Integrating
this we get 
Hence, The
General Solution is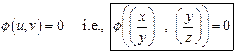 
.
23)
Find the
particular integral of 
.
Solution:
Hence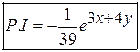 
24)
Solve 
Solution:
The given equation is of the 
The
complete integral is 
where
Now 
The
complete integral is 
.
.
25)
Form the p.d.e by eliminating a and b from 
.
Solution:
Given 
Differentiating the above equation p.w.r.to and
,
From
&
we
get, 
26)
Solve 
.
Solution:
Given, 
.
This is of the form 
Let
Substitute
these values in 
.
27)
Give the general
solution of 
.
Solution:
Given,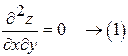 
Integrating
with respect to ,
we get 
Again
Integrating with respect to ,
.
Here
and
are
arbitrary functions of and
respectively.
28)
Solve 
.
Solution:
Here
The
solution is 
29)
Form the partial
differential equation by eliminating 
from
the relation 
.
Solution:
Given, 
Differentiating
p.w.r.to we
get
Differentiating
p.w.r.to we
get
From
&
we
get, 
.
.
**********************
| Earning: Approval pending. |
