Anna University Coimbatore 2009 B.E Transforms and Partial Differential Equations( 2 ks with Answers for Unit-1) - Question Paper
TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS
UNIT-I
FOURIER SERIES
TWO MARKS
1)
Determine ![]() in
the Fourier series expansion of
in
the Fourier series expansion of ![]() in
in
![]() with
period
with
period ![]() .
.
Solution:
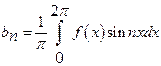
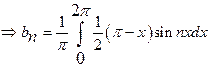
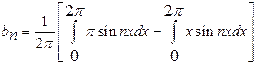
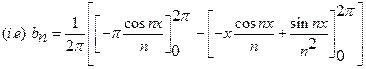
![]()
![]()
2)
Define root
mean square value of ![]() in
in
![]() .
.
(OR) Define root mean square value of a function ![]() over
the range (a,b) .
over
the range (a,b) .
Solution:
Let ![]() be
the function defined in the interval
be
the function defined in the interval ![]() then
then
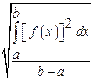 is
called the Root Mean Square value and is denoted by
is
called the Root Mean Square value and is denoted by ![]() .
.
The RMS value is otherwise known as Effective value 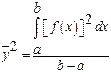 .
.
3)
If ![]() and
and
![]() for
all x,
for
all x,
find the sum of the Fourier series of ![]() at
at
![]() .
.
Solution:
Sum of the Fourier Series
![]()
4)
Find the
value of ![]() in
the cosine series expansion of
in
the cosine series expansion of ![]() in
the interval (0,10).
in
the interval (0,10).
Solution:
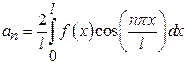
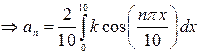
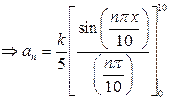
![]()
5)
Find the
root mean square value of the function ![]() in
the interval ( 0, l ).
in
the interval ( 0, l ).
Solution:
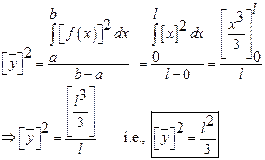
6) State Dirichlets conditions for a given function to expand in Fourier series.
(OR) State the Dirichlets condition for the convergence of the Fourier series of
![]() in
in
![]() with
period
with
period ![]() .
.
Solution:
Any function ![]() can
be developed as a Fourier series
can
be developed as a Fourier series 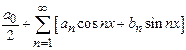 where
where
![]() are
constants provided
are
constants provided
![]() is
a periodic, single valued, finite.
is
a periodic, single valued, finite.
![]() is
continuous with finite number of discontinuities in any one period.
is
continuous with finite number of discontinuities in any one period.
![]() has
atmost finite number of maxima and minima.
has
atmost finite number of maxima and minima.
7)
If the
Fourier series of the function ![]() in
the interval
in
the interval
![]() is
is
![]() ,
then find the value of the infinite series
,
then find the value of the infinite series ![]()
Solution:
Here ![]() is
a point of discontinuity. Sum of Fourier series
is
a point of discontinuity. Sum of Fourier series![]()
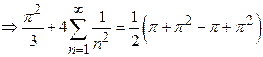
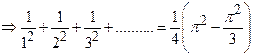
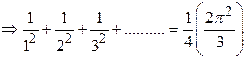
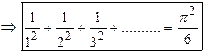
8)
Find the
Fourier sine series of the function ![]() ,
,
![]() .
.
Solution:
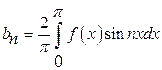
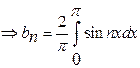
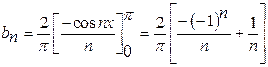
![]()
9)
If the
Fourier series of the function 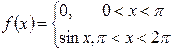 is
is
![]() deduce
that
deduce
that ![]() .
.
Solution:
Here ![]() is
a point of continuity. Sum of Fourier series
is
a point of continuity. Sum of Fourier series![]()
![]()
![]()
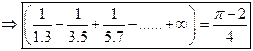
10)
Does ![]() possess
a Fourier expansion ?
possess
a Fourier expansion ?
Solution:
Here ![]() is
a Periodic function with period
is
a Periodic function with period ![]() ,
not
,
not ![]() and
it does not satisfy the Dirichlets condition.
and
it does not satisfy the Dirichlets condition.
11) State Parsevals Theorem on Fourier series. (OR) State Parsevals identity of Fourier series.
Solution:
If ![]() is
expressed as a Fourier series of periodicity
is
expressed as a Fourier series of periodicity ![]() in
in
![]() then
then
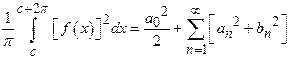 .
.
12)
Find ![]() in
the expansion of
in
the expansion of ![]() as
a Fourier series in
as
a Fourier series in ![]() .
.
Solution:
Here ![]()
![]()
![]()
So,
![]() is
an Even function. Hence
is
an Even function. Hence ![]() .
.
13)
If ![]() is
an odd function defined in ( -l , l ) , what are the values of
is
an odd function defined in ( -l , l ) , what are the values of
![]() and
and
![]() ?
?
Solution:
Here ![]() is
an Odd function in
is
an Odd function in ![]() .
So
.
So ![]() and
and
![]() .
.
14)
Find the
constant term in the Fourier series corresponding to ![]() expressed
in the interval
expressed
in the interval ![]() .
.
Solution:
It
is an Even function. So ![]()
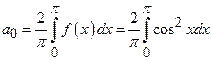
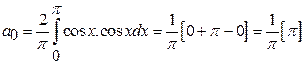
![]()
15)
To which
value the Half range sine series corresponding to ![]() expressed
in the interval (0,2) converges to
expressed
in the interval (0,2) converges to ![]() ?
?
Solution:
Here ![]() is
a point of discontinuity. Sum of Fourier series
is
a point of discontinuity. Sum of Fourier series![]()
i.e., Sum of Fourier series![]()
16)
If ![]() is
expressed as a Fourier series in the interval ( - 2, 2 ) to which value this
series converges at
is
expressed as a Fourier series in the interval ( - 2, 2 ) to which value this
series converges at ![]() ?
?
Solution:
Here ![]() is
a point of discontinuity.
is
a point of discontinuity.
![]() Sum
of Fourier series
Sum
of Fourier series![]()
17)
If the
Fourier series corresponding to ![]() in
the interval
in
the interval ![]() is
is
![]() ,without
finding the values of
,without
finding the values of ![]() Find
the value of
Find
the value of ![]()
Solution:
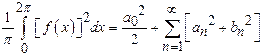
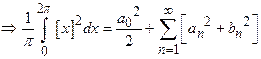
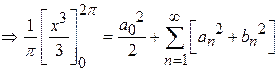
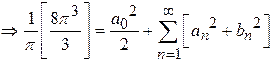
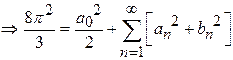 .
Hence
.
Hence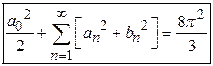 .
.
18)
Find the
Half range sine series for ![]() in
in
![]() .
.
Solution:
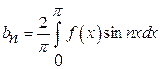
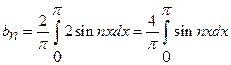
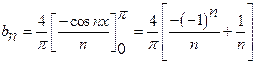
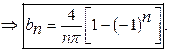
19)
If the
cosine series for ![]() for
for
![]() is
given by
is
given by 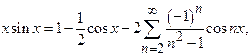 Prove
that
Prove
that ![]() .
.
Solution:
Here ![]() is
a point of continuity.
is
a point of continuity.
Sum of Fourier series ![]()
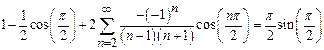
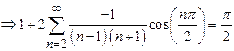
![]()
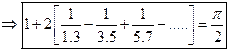
20) What do you mean by Harmonic analysis? (OR) Define Harmonic analysis.
Solution:
The process of finding the Fourier series for a function given by
Numerical value is known as Harmonic Analysis,
![]() 2[Mean
value of
2[Mean
value of ![]() in
in
![]()
![]() 2[Mean
value of
2[Mean
value of ![]() in
in
![]()
![]() 2[Mean
value of
2[Mean
value of ![]() in
in
![]() .
.
21)
In the
Fourier expansion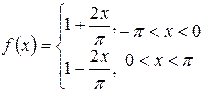 in
in![]() ,
find the value of
,
find the value of ![]() ,the
coefficient of
,the
coefficient of ![]()
Solution:
Here ![]() is
an Even function. So
is
an Even function. So ![]() .
.
22)
Find ![]() in
expanding
in
expanding ![]() as
Fourier series in
as
Fourier series in![]() .
.
Solution:
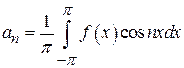
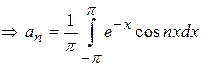
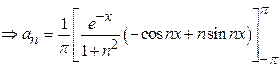
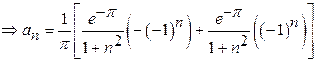
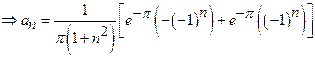
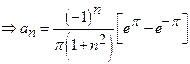
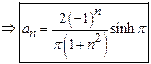
23)
If ![]()
![]() in
in
![]() ,
find the sum of the series
,
find the sum of the series 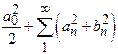
Solution:
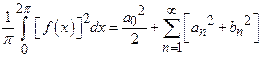
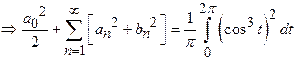
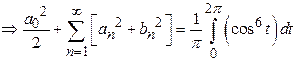
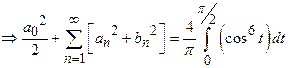
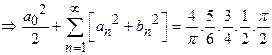
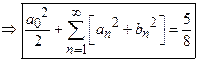
24)
The Fourier
series of ![]() in
(0,2) and that of
in
(0,2) and that of ![]() in
(-2,0) are identical or not. Give reason.
in
(-2,0) are identical or not. Give reason.
Solution:
For ![]()
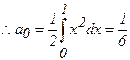 ,
,
For ![]()
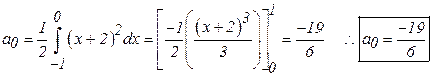
Since ![]() for
for
![]() and
and
![]() for
for
![]() are
not equal, hence their Fourier series are not identical.
are
not equal, hence their Fourier series are not identical.
25)
Define the
value of the Fourier series of ![]() at
a point of discontinuity.
at
a point of discontinuity.
Solution:
![]() is
defined in
is
defined in ![]() .
.
Sum of Fourier series![]() If point of discontinuity is at
If point of discontinuity is at ![]() .
.
Sum of Fourier series![]() .
.
26)
If ![]() is
defined in
is
defined in ![]() ,
write the values of Fourier coefficients
,
write the values of Fourier coefficients ![]() and
and
![]() .
.
Solution:
![]()
![]()
![]() .
So, it is an Odd function
.
So, it is an Odd function
Hence, the values of ![]() and
and
![]() .
.
27)
If ![]() in
in
![]() ,
prove that
,
prove that ![]() .
.
Solution:
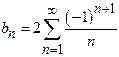
By Parsevals identity, 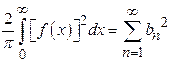
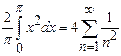
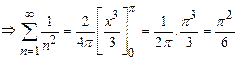
![]()
28)
The
functions ![]() ,
,
![]() cannot
be expanded as a
cannot
be expanded as a
Fourier series. Why ?
Solution:
It does not satisfy the Dirichlets condition. So, it is not possible to
expand the function as Fourier series.
29)
Expand the
function ![]() ,
,![]() as
a series of sines.
as
a series of sines.
Solution:
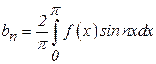
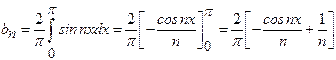
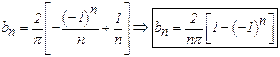
30)
Find the
Fourier Cosine series of ![]() ,
,
![]() .
.
Solution:
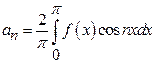
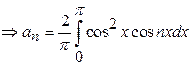
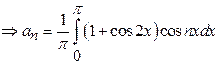
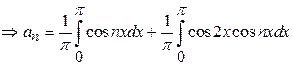
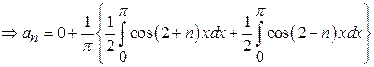
![]()
![]()
31)
![]() ,
,
![]() which
one of the following is correct a) an even function b) an odd function
c) neither even nor odd
which
one of the following is correct a) an even function b) an odd function
c) neither even nor odd
Solution:
c) neither even nor odd
(
![]() is
Even function only in the interval
is
Even function only in the interval ![]() .But
here the interval is
.But
here the interval is ![]() ).
).
32)
Let ![]() be
defined in
be
defined in ![]() by
by
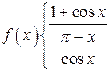
![]()
![]() and
and
![]() .
Find the value of
.
Find the value of ![]() .
.
Solution:
Sum of Fourier series![]()
*********************
| Earning: Approval pending. |
