Anna University Coimbatore 2009 B.E Two k with Answers for Transforms and Partial Differential Equations( Unit-2) - Question Paper
TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS
ANNA UNIVERSITY (2 Marks) QUESTIONS WITH ANSWERS
UNIT-II
FOURIER TRANSFORM
TWO MARKS
1) Write the Fourier transform pair.
Ans :Let f(x) be a given function
defined in (-∞,+∞) then the fourier transform is given by 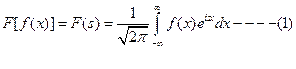 corresponding
inverse formula is given by
corresponding
inverse formula is given by ![]() .
Equation (1) & (2) jointly called as fourier transform pair.
.
Equation (1) & (2) jointly called as fourier transform pair.
2)
If ![]() is
the Fourier cosine transform of f(x), prove that the Fourier cosine
transform of f(ax) is
is
the Fourier cosine transform of f(x), prove that the Fourier cosine
transform of f(ax) is 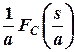 .
.
Ans : we know that 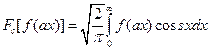 .
.
Put ![]() then
then
![]()
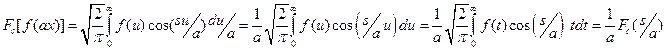
3) If F(S) is Fourier transform of f(x), write the Fourier transform of f(x)cos(ax) in terms of F.
Ans: ![]()
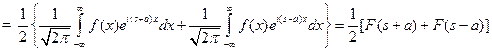
4) State the Convolution theorem for Fourier transforms.
Ans: The Fourier transform of the
convolution of ![]() is
the product of their Fourier transform.
is
the product of their Fourier transform. ![]() .
.
5) If F(S) is Fourier transform of f(x), then find the Fourier transform of f(x-a).
Ans : 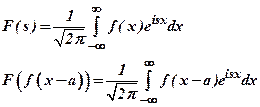
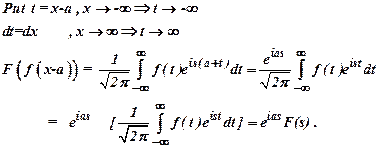
6)
If ![]() is
the Fourier Sine transform of f(x), show that
is
the Fourier Sine transform of f(x), show that ![]() .
.
Ans: 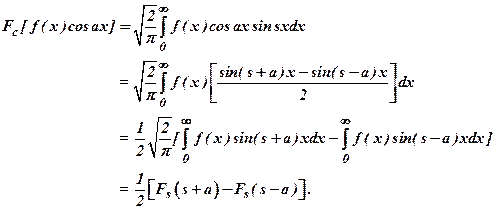
7)
Solve the integral
equation ![]() .
(April 2004)
.
(April 2004)
Ans :
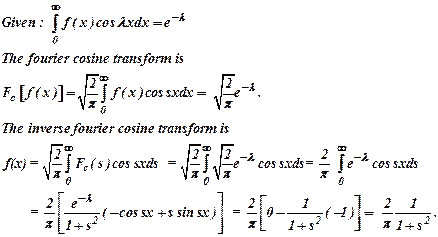
8)
Find the Fourier
transform of f(x) if ![]()
![]()
![]() .
(April 2004)
.
(April 2004)
Ans : 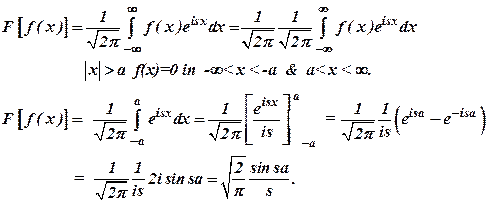
9)
Find the Fourier
cosine transform of ![]() .
(Nov 2004)
.
(Nov 2004)
Ans :
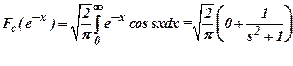
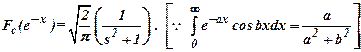
10)
Find a) ![]() and
b)
and
b) 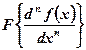 in
terms of the Fourier transform of f
in
terms of the Fourier transform of f 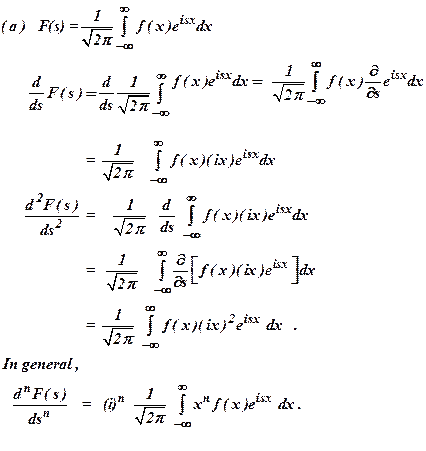
(b)
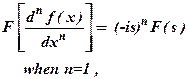
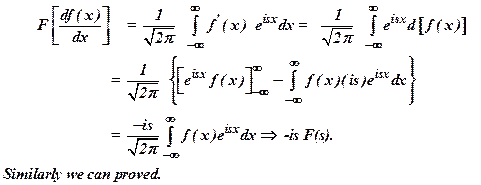
11) State Fourier integral theorem. (April 2005) (May/June 2009)
Ans
: 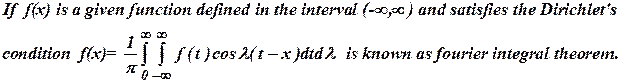
12)
Find the Fourier
Sine transform of ![]() .
(April 2005),(Dec 2008)
.
(April 2005),(Dec 2008)
Ans
: 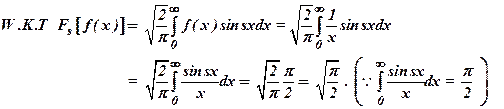
13)
Find the Fourier
transform of ![]() .
(Nov/Dec 2005)
.
(Nov/Dec 2005)
Ans:![]()
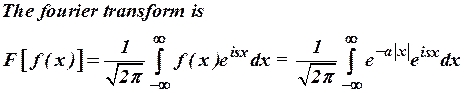
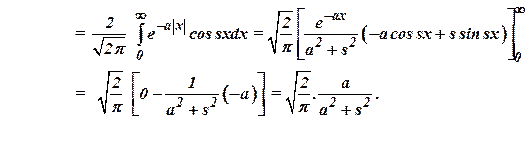
14)
Find the Fourier
cosine integral representation of ![]()
![]() .
.
Ans
: 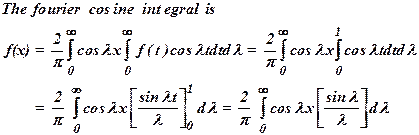
15)
Find the Fourier
Sine transform of f(x)= ![]() .
(May 2006)
.
(May 2006)
Ans
: 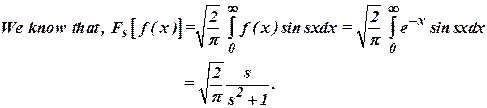
16)
Prove that ![]() ,
a>0. (May 2006)
,
a>0. (May 2006)
Ans
: 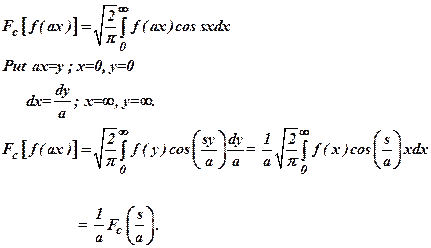
17)
If ![]() then
give the value of
then
give the value of ![]() .
(May 2006)
.
(May 2006)
Ans : Sama as 16
18)
Find the Fourier
transform of ![]()
![]() .
(May 2006)Ans :
.
(May 2006)Ans : 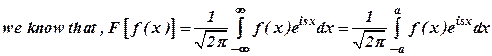
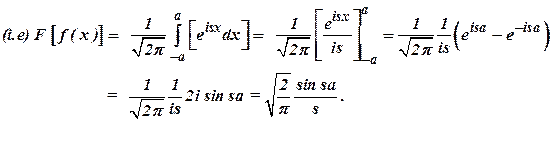
19) Find the Fourier cosine transform of f(x) defined as
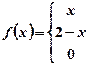
![]()
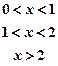 .
(Nov/Dec 2006) Ans
:
.
(Nov/Dec 2006) Ans
: 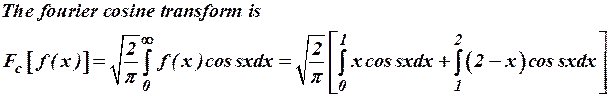
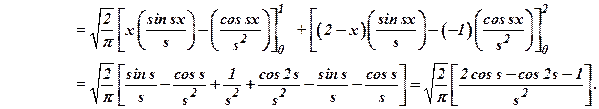
20)
P.T ![]() where
where
![]() .
(M/J 2007)
.
(M/J 2007)
Ans
: 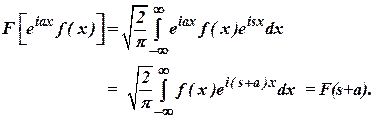
21) Write down the Fourier cosine transform pair formulae. (M/J 2007)
Ans:
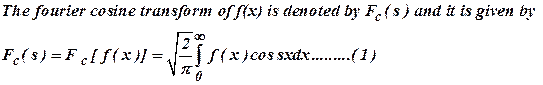
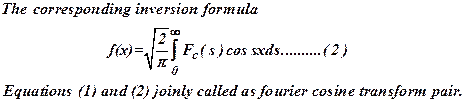
22)
If ![]() prove
that
prove
that ![]() .
(N/D 2003),(Nov 2005)
.
(N/D 2003),(Nov 2005)
Ans : 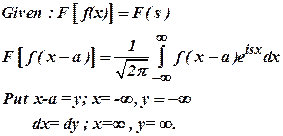
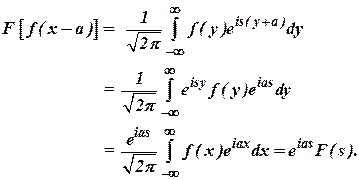
23)
Prove that if ![]() ,
then
,
then ![]() (Dec
2008)
(Dec
2008)
Ans : 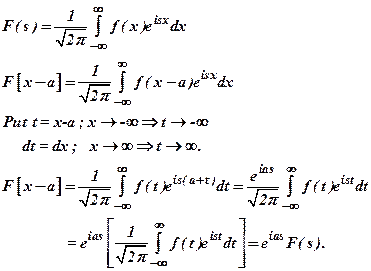
24)
Find the Fourier
transform of ![]() defined
by
defined
by
![]()
![]()
![]() .(Dec
2008)
.(Dec
2008)
Ans: 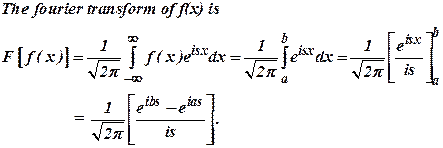
25)
Find the Fourier
Cosine transform of ![]()
![]()
![]() . (Dec
2008)
. (Dec
2008)
Ans : 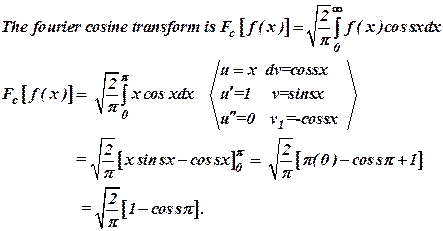
26)
If ![]() , prove
that
, prove
that 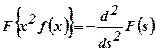 . (Dec
2008)
. (Dec
2008)
Ans : By property, 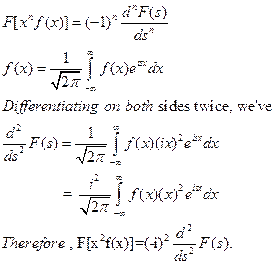
27)
Find the Fourier
sine transform of ![]() .
(Dec 2008)
.
(Dec 2008)
Ans : We know that , 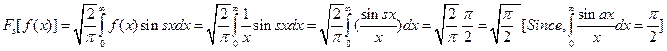
28) State Parsevals identity on complex Fourier transforms. (Dec 2008)
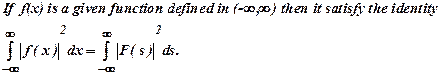
29)
If ![]() then
prove that
then
prove that ![]() .
(Dec 2008)
.
(Dec 2008)
Ans : 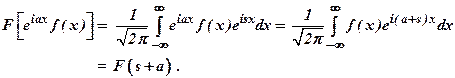
30) State Modulation theorem in Fourier transform. (Dec 2008)
Ans : 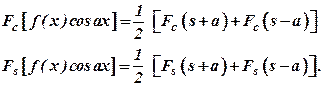
31) Give a function which is self reciprocal under Fourier sine and cosine transforms. (Dec 2008)
Ans : 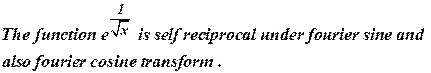
32)
If ![]() ,
then prove that
,
then prove that ![]() .
(Dec 2008)
.
(Dec 2008)
Ans : 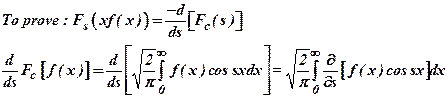

****************************************
| Earning: Approval pending. |
