Anna University Coimbatore 2009 B.E 2 ks with Answers for TPDE (Unit-4) - Question Paper

TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS

 

POSSIBLE TWO MARKS QUESTIONS WITH ANSWERS

UNIT-IV

APPLICATIONS OF PDE

 

TWO MARKS

 

1) Classify the following second order partial differential equations:

i).

Ans:

Therefore , the given PDE is parabolic.

ii) .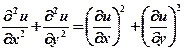

Ans:

Therefore, the given PDE is ellipse.

iii) .

Ans :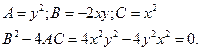

Therefore, the given PDE is parabolic.

iv) .

Ans: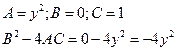

Therefore, the given equation is elliptic, if or

v) .

Ans:

Therefore , the given equation is elliptic if. hyperbolic if & parabolic if

2) Classify the partial differential equations .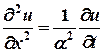

Ans: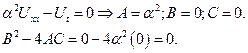

The given equation is parabolic.

3)        Classify the following PDE i) .

Ans: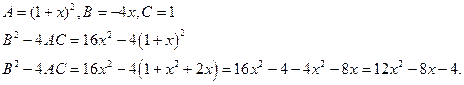

If [Parabolic equation ]

If (or) , [Hyperbolic equation].

ii) .

Ans: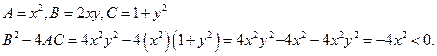

Therefore the equation is ellipse.

4)        What is the constant in the wave equation ?

Ans : .

5)        In the diffusion equation 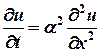what does stand for?

Ans : where , and

6)        What is the basic difference between the solutions of one dimensional wave equation and one dimensional heat equation?

Ans : The solution of one dimensional wave equation is of periodic in nature. But the solution of heat flow equation is not periodic in nature.

7)        What are the possible solutions of one dimensional wave equation?

Ans: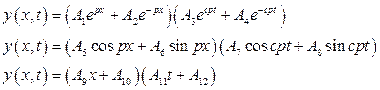

8)        Explain the various variables involved in one dimensional wave equation.

Ans : One dimensional wave equation is , x and t are the two

variables , where x denotes the length and t denotes the time.

9)        A tightly stretched string of length 2L is fastened at both ends. The midpoint of the string is displaced to a distance b and released from rest in this position. Write the initial conditions.

Ans :

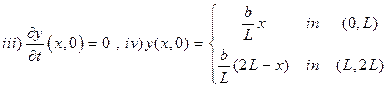
10)     Write the initial conditions of the wave equation if the string has an initial displacement but no initial velocity.

Ans :

11)     Write the boundary conditions and initial conditions for solving the vibration of string equation , if the string is subjected to initial displacement f(x) and initial velocity g(x).

Ans :

12)     State one dimensional heat equation with initial and boundary conditions.

Ans : The one dimensional heat equation is . The boundary

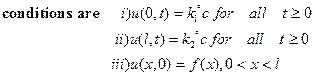
13)     In steady state conditions derive the solution of one dimensional heat flow equation.

Ans : The one dimensional heat equation is . In steady state , temperature u depends only on x and not time t. Therefore The equation is , the solution is

14)     An insulated rod of length 60 cm has is ends A and B maintained at and respectively. Find the steady state solution of the rod.

Ans : The solution is Apply (i) boundary condition, we get b=20.

Apply (ii) boundary condition , Therefore

15)     A rod 30 cm long has its ends A and B kept at and respectively until steady state conditions prevail. Find the steady state temperature in the rod.

Ans : The solution is Apply (i) b.c, we get b=20. Applying (ii) b.c, we get 80=30a+20,a=2. Therefore u(x)=2x+20.

16)     State Fourier law of heat conduction.

Ans : The rate at which heat flows across any area is proportional to the area and to the

temperature gradient normal to the curve . This constant of proportionality is known

as the thermal

conductivity (k) of the material.

17)     What are the possible solutions of one dimensional heat equation?

Ans :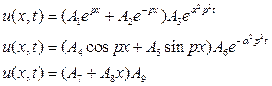

18)     How many boundary conditions are required to solve completely

Ans : The conditions are there.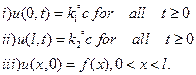

19)     Write the steady state heat flow equation in two dimension in Cartesian & Polar form. Ans : 1. Cartesian form : .

2. Polar form : .

20)     Write any two solutions of the Laplace equation obtained by the method of separation of variables.

Ans :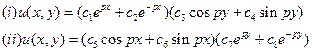

21)     In two dimensional heat flow, the temperature at any point is independent of which coordinate?

Ans : In two dimensional heat flow , the temperature at any point is independent of Z co-

ordinate.

22)     Explain the term steady state.

Ans : The state in which temperature does not vary with respect to time t is called steady

state.

23)     Classify the p.d.e

Ans :

Therefore it is hyperbolic equation.

24)     State the empirical laws used in deriving one-dimensional heat flow equation.

Ans : (i) Heat flows from a higher temperature to lower temperature .

(ii) The amount of heat required to produce a given temperature

change in a body is proportional to mass of the body and the

temperature change.

25)     Write the product solutions of .

Ans :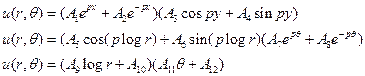

26)     What is the equation governing the two dimensional heat flow steady state and also write its solution.

Ans : The equation The equation is

.

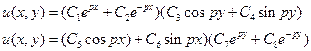27)     Classify the p.d.e .

Ans : A=1,B=2,C=1.

28)     Write the various possible solutions of the Laplace equation in two dimensions.

Ans :

29)     A infinitely long uniform plate is bounded by the edges and the ends right angles to them. The breadth of the edges is l and is maintained at . All the other edges are kept at Write down the boundary condition in mathematical form.

Ans :

 

30)     Write any two assumptions made while deriving the partial differential equation of transverse vibrations of a string.

Ans : (i) The mass of the string per unit length is constant.

(ii) The string is perfectly elastic and does not offer any resistance to bending.

31)     Define steady state. Write the one dimensional heat equation in steady state.

Ans : The state in which temperature does not vary with respect to time t is

called steady state one dimensional heat equation in steady state is .

32)     Write all the solutions of Laplace equation in Cartesian form, using the method of separation of variables.

Ans :

33)     Verify that is a solution of

Ans: Consider 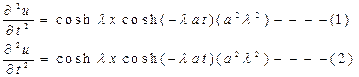From (1) and (2) ,

Hence is a solution of

*****************************************