Anna University Coimbatore 2009 B.E 2 ks with Answers for TPDE (Unit-5 Z-Transforms) - Question Paper
TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS
POSSIBLE TWO MARKS QUESTIONS WITH ANSWERS
UNIT -V
Z-TRANSFORM
TWO MARKS
1)
Find ![]() in
Z-transform.
in
Z-transform.
Solution:
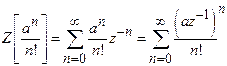
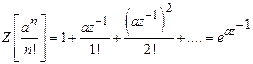
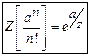 .
.
2)
Find ![]() using
Z-transform.
using
Z-transform.
Solution:
![]()
![]()
![]() .
.
3) State and prove initial value theorem in Z-transform.
Solution:
Statement:
If ![]() then
then
![]()
![]() .
.
Proof:
![]()
![]()
![]()
![]()
![]()
![]()
4)
Find the
Z-transform of ![]()
Solution:
![]()
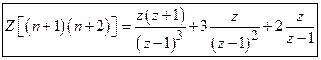
5)
Find the
Z-transform of ![]()
Solution:
![]()
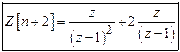 .
.
6) State the final value theorem in Z-transform.
Solution:
Statement:
If ![]() then
then
![]()
![]() .
.
Proof: Refer Text Book
7)
Find ![]() .
.
Solution:
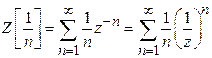
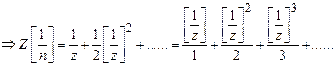
![]()
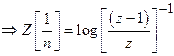
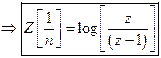
8)
Evaluate ![]() .
.
Solution:
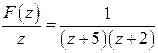
![]()
Consider,
![]()
![]()
![]()
![]()
Put
![]() in
in
![]() ,
,
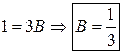
Similarly,
Put ![]() in
in
![]() ,
,
![]()
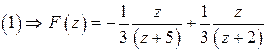
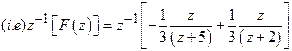
![]()
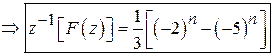 .
.
9)
Prove that ![]() .
.
Solution:
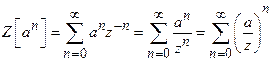
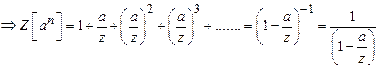
![]() .
.
10)
Prove that ![]() .
.
Solution:
W.K.T.,
![]() .
Here
.
Here ![]()
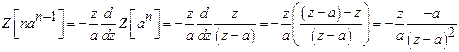
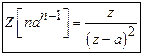 .
.
11)
Prove that ![]() .
.
Solution:
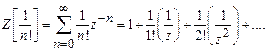
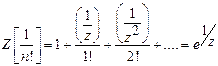
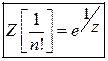 or
or
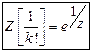 .
.
12)
Find ![]() .
.
Solution:
![]()
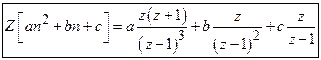
13)
Find the initial
and final values of the function ![]() .
.
Solution:
By Initial Value Theorem, ![]()
![]() .
.
By Final Value Theorem, ![]()
![]() .
.
14)
Find the
Z-transform of i) ![]() ii)
ii)
![]() iii)
iii)
![]() iv)
iv)
![]() .
.
Solution:
i) ![]()
![]() .
The ROC is
.
The ROC is ![]() .
.
ii) ![]()
![]()
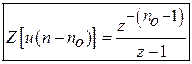 .
The ROC is
.
The ROC is ![]() .
.
iii) ![]()
W.K.T.,
![]()
Here
![]() ,
Therefore,
,
Therefore, ![]()
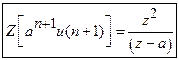
iv) ![]() .
.
![]()
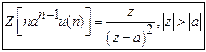 .
.
15)
What is the
Z-transform of ![]() .
.
Solution:
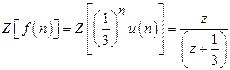
![]()
16) State the convolution property of Z-transform.
Solution:
i)![]()
Where ![]()
ii) ![]()
Where ![]() .
.
17) State and prove shifting theorem of Z-transform.
Solution:
Statement:
First Shifting Theorem,
If ![]() then
then
![]() .
.
Second Shifting Theorem,
If ![]() then
then
![]() .
.
Proof: Refer text book
18)
Find the
Z-transform of ![]() .
.
Solution:
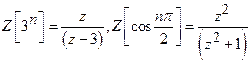
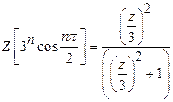
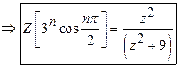
19)
Find the
Z-transform of ![]()
Solution:
W.K.T., 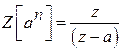
![]() (By
Linearity Property )
(By
Linearity Property )
![]()
![]()
20)
Prove that ![]()
![]() .
.
Solution:
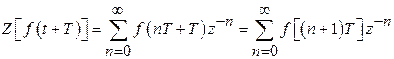
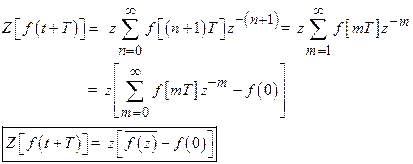
21)
Find the
Z-transform of ![]() .
.
Solution:
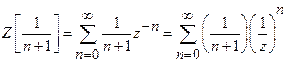
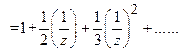
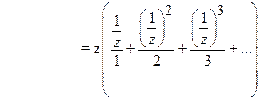
![]()
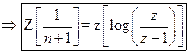
22)
Prove that 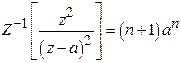
Solution:
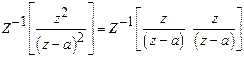
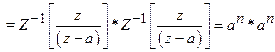
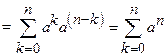
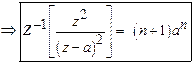
23)
Find the
difference equation from ![]()
Solution:
![]()
![]()
![]()
![]()
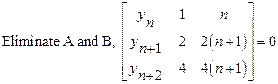
![]()
24)
Find ![]() .
.
Solution:
![]()
![]()
![]()
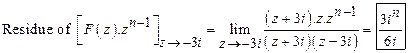
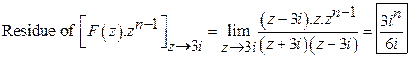
![]()
![]() .
.
25) Define unit impulse sequence and find its Z-transform.
Solution:
A discrete unit impulse function is defined by ![]() .
Therefore,
.
Therefore, 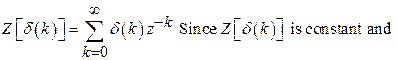
![]()
![]()
26) Define convolution of two sequences.
Solution:
![]()
![]()
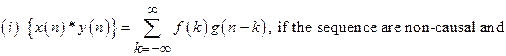
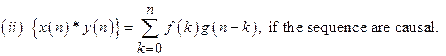
27)
Find the
inverse Z-transform of ![]()
Solution:
W.K.T.,
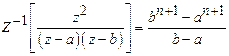 .
Here
.
Here ![]() ,
,
![]()
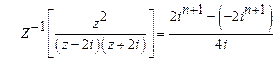
![]()
![]()
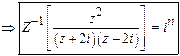
28)
From the
difference equation of ![]() ,find
,find
![]() in
terms of
in
terms of ![]() .
.
Solution:
Taking Z-Transform on both sides
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
29)
Find ![]() ,where
,where
![]() for
n= 0, 1, 2, .
for
n= 0, 1, 2, .
Solution:
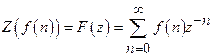
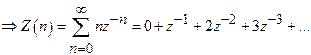
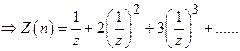
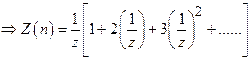
![]()
![]()
***********************
| Earning: Approval pending. |
