Institute of Actuaries of India 2005 CT5-Contingencies,Core Technical - Question Paper
Faculty of Actuaries Institute of Actuaries
7 September 2005 (pm)
Subject CT5 Contingencies Core Technical
Time allowed: Three hours INSTRUCTIONS TO THE CANDIDATE
1. Enter all the candidate and examination details as requested on the front of your answer booklet.
2. You must not start writing your answers in the booklet until instructed to do so by the supervisor.
3. Mark allocations are shown in brackets.
4. Attempt all 13 questions, beginning your answer to each question on a separate sheet.
5. Candidates should show calculations where this is appropriate.
Graph paper is not required for this paper.
ATTHE END OF THE EXAMINATION
Hand in BOTH your answer booklet, with any additional sheets firmly attached, and this question paper.
In addition to this paper you should have available the 2002 edition ofthe Formulae and Tables and your own electronic calculator.
1 Describe what is meant by adverse selection in the context of a life insurance
companys underwriting process and give an example. [2]
2 Describe how occupation affects morbidity and mortality. [3]
3 A graph of f0(t), the probability density function for the random future lifetime, T0, is plotted on the vertical axis, with t plotted on the horizontal axis, for data taken from the English Life Table No. 15 (Males).
You are given that f0(t) = tp0 nt. You observe that the graph rises to a peak at around t = 80 and then falls.
Explain why the graph falls at around t = 80 . [3]
4 Calculate the value of 1 75 p45 5 on the basis of mortality of AM92 Ultimate and assuming that deaths are uniformly distributed between integral ages. [3]
5 A population is subject to a constant force of mortality of 0.015.
Calculate:
(a) The probability that a life aged 20 exact will die before age 21.25 exact.
(b) The curtate expectation of a life aged 20 exact.
[4]
6 Define a(12) , fully in words and calculate its value using PMA92C20 and
60:50:201 J &
PFA92C20 tables for the two lives respectively at 4% interest. [5]
7 A life insurance company prices its long-term sickness policies using the following three-state continuous-time Markov model, in which the forces of transition a, p, (J. and u are assumed to be constant:
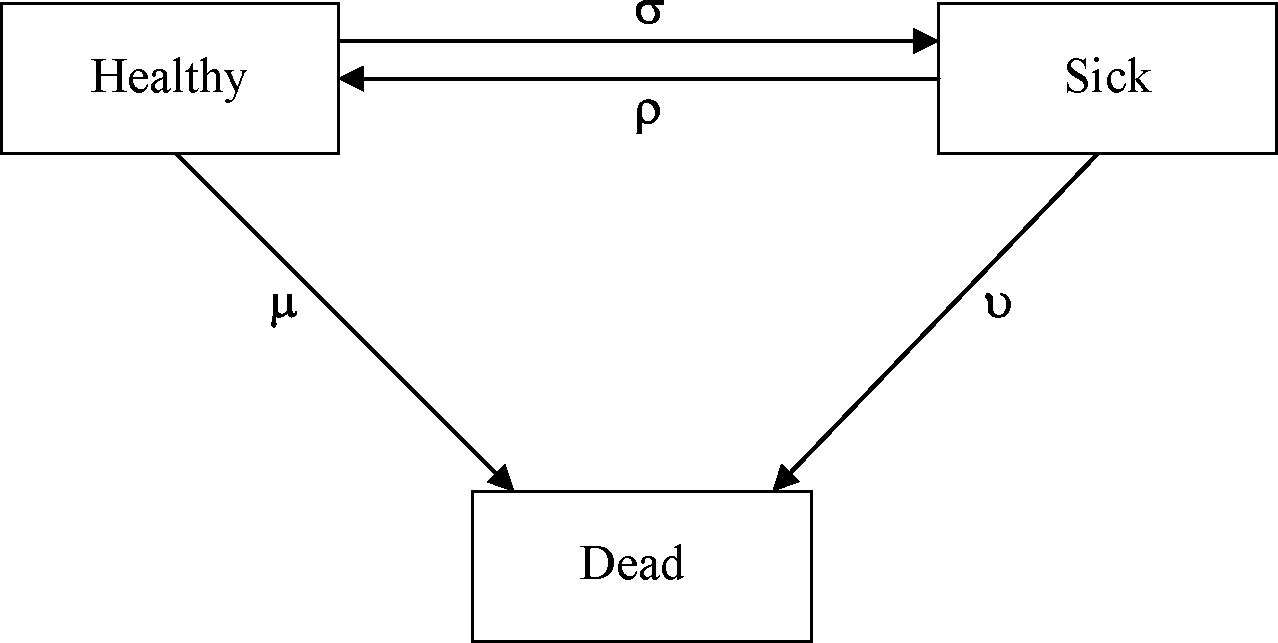
The company issues a particular long-term sickness policy with a benefit of 10,000 per annum payable continuously while sick, provided that the life has been sick continuously for at least one year. Benefit payments under this policy cease at age 65 exact.
Write down an expression for the expected present value of the sickness benefit for a healthy life aged 20 exact. Define the symbols that you use.
[5]
8 A life insurance company issues an annuity contract to a man aged 65 exact and his wife aged 62 exact. Under the contract, an annuity of 20,000 per annum is guaranteed payable for a period of 5 years and thereafter during the lifetime of the man. On the mans death, an annuity of 10,000 per annum is payable to his wife, if she is then alive. This annuity commences on the monthly payment date next following, or coincident with, the date of his death or from the 5th policy anniversary, if later and is payable for the lifetime of his wife. Annuities are payable monthly in advance.
Calculate the single premium required for the contract.
Basis:
Mortality PMA92C20 for the male and PFA92C20 for the female Interest 4% per annum
Expenses none [9]
9 A life insurance company issues an annuity policy to two lives each aged 60 exact in return for a single premium. Under the policy, an annuity of 10,000 per annum is payable annually in advance while at least one of the lives is alive.
(i) Write down an expression for the net future loss random variable at the outset for this policy. [2]
(ii) Calculate the single premium, using the equivalence principle.
Basis:
Mortality PMA92C20 for the first life, PFA92C20 for the second life Interest 4% per annum
Expenses ignored [3]
(iii) Calculate the standard deviation of the net future loss random variable at the outset for this policy, using the basis in part (ii).
You are given that 36060 = 11.95 7 at a rate of interest 8.16% per annum. [4]
[Total 9]
10 A life insurance company issued a with profits whole life policy to a life aged 20 exact, on 1 July 2002. Under the policy, the basic sum assured of 100,000 and attaching bonuses are payable immediately on death. The company declares simple reversionary bonuses at the start of each year. Level premiums are payable annually in advance under the policy.
(i) Give an expression for the gross future loss random variable under the policy at the outset. Define symbols where necessary. [3]
(ii) Calculate the annual premium, using the equivalence principle.
Basis:
Mortality Interest Bonus loading Expenses Initial
AM92 Select 6% per annum 3% simple per annum 200
Renewal 5% of each premium payable in the second and subsequent years
Assume bonus entitlement earned immediately on payment of premium.
[4]
On 30 June 2005 the policy is still in force. A total of 10,000 has been declared as a simple bonus to date on the policy.
(iii)
The company calculates provisions for the policy using a gross premium prospective basis, with the following assumptions:
Mortality Interest Bonus loading Renewal expenses
AM92 Ultimate 4%
4% per annum simple 5% of each premium
Calculate the provision for the policy as at 30 June 2005.
[4]
[Total 11]
11 A life insurance company issues a three-year unit-linked endowment assurance
contract to a male life aged 62 exact under which level annual premiums of 10,000 are payable in advance throughout the term of the policy or until earlier death. 85% of each years premium is invested in units at the offer price.
There is a bid-offer spread in unit values, with the bid price being 95% of the offer price.
There is an annual management charge of 1.25% of the bid value of units. Management charges are deducted at the end of each year, before death or maturity benefits are paid.
On the death of the policyholder during the term of the policy, there is a benefit payable at the end of the year of death of 20,000, or the bid value of the units allocated to the policy, if greater. On maturity, 115% of the full bid value of the units is payable.
The company holds unit provisions equal to the full bid value of the units. It sets up non-unit provisions to zeroise any negative non-unit fund cashflows, other than those occurring in the first year.
The life insurance company uses the following assumptions in carrying out profit tests of this contract:
Mortality
AM92 Ultimate
Expenses Initial 600
Renewal 100 at the start of each of the second and third policy years
Unit fund growth rate 8% per annum
Non-unit fund
interest rate
4% per annum
Non-unit fund
provision basis AM92 Ultimate mortality, interest 4% per annum
Risk discount rate 15% per annum
Calculate the profit margin on the contract.
[14]
12 On 1 January 2000, a life insurance company issued joint life whole life assurance policies to couples. Each couple comprised one male and one female life and both were aged 50 exact on 1 January 2000. Under each policy, a sum assured of 200,000 is payable immediately on the death of the second of the lives to die.
Premiums under each policy are payable annually in advance while at least one of the lives is alive.
(i) Calculate the annual premium payable under each policy. Basis:
PMA92C20 for the male PFA92C20 for the female
Mortality
Interest
Initial
Renewal
Expenses
4% per annum 1,000
5% of each premium payment
[5]
(ii) On I January 2004, 5,000 of these policies were still in force. Under 100 of these policies only the female life was alive. Both lives were alive under the other 4,900 policies.
The company calculates provisions for the policies on a net premium basis, using PMA92C20 and PFA92C20 mortality for the male and female lives respectively and 4% per annum interest.
During the calendar year 2004, there was one claim for death benefit, in respect of a policy where the female life only was alive at the start of the year. In addition, one male life died during the year under a policy where both lives were alive at the start of the year. 4,999 of the policies were in force at the end of the year.
Calculate the mortality profit or loss for the group of 5,000 policies for the calendar year 2004. [9]
[Total 14]
13 Under the rules of a pension scheme, a member may retire due to age at any age from exact age 60 to exact age 65.
On age retirement, the scheme provides a pension of 1/60th of Final Pensionable Salary for each year of scheme service, subject to a maximum of 40/60ths of Final Pensionable Salary. Only complete years of service are taken into account.
Final Pensionable Salary is defined as the average salary over the three-year period before the date of retirement.
The pension scheme also provides a lump sum benefit of four times Pensionable Salary on death before retirement. The benefit is payable immediately on death and Pensionable Salary is defined as the annual rate of salary at the date of death.
You are given the following data in respect of a member:
Date of birth 1 January 1979
Date of joining the scheme 1 January 2000
Annual rate of salary at 1 January 2005 50,000
Date of last salary increase 1 April 2004
(i) Derive commutation functions to value the past service and future service pension liability on age retirement for this member as at 1 January 2005. State any assumptions that you make and define all the symbols that you use.
[12]
(ii) Derive commutation functions to value the liability in respect of the lump sum payable on death before retirement for this member as at 1 January 2005.
State any assumptions that you make and define all the symbols that you use.
[Total 18]
CT5 S20058
|
Attachment: |
| Earning: Approval pending. |
