Sathyabama University 2008 B.E Chemical Engineering Fluid mechanics - Question Paper
SATHYABAMA UNIVERSITY
(Established under section 3 of UGC Act, 1956)
Course & Branch: B.E/ B.Tech - CSE/ECE/EEE/MECH/CIVIL/
CHEM (Part Time)
Title of the paper: Engineering Mathematics - I
Semester: I Max. Marks: 80
Sub.Code: 6CPT0006 (2007/2008 JAN) Time: 3 Hours
Date: 13-05-2008 Session: FN
PART A (10 x 2 = 20)
Answer All the Questions
1. Differentiate: x2 sin 3x.
2. State Eulers theorem on partial derivatives of a Homogenous function.
3. Evaluate: 
log x dx.
4. State any two properties of definite integrals.
5. Define: Analytic function.
6. State Cauchys Integral theorem.
7. Define: Conformal Mapping.
8. Find the Residues of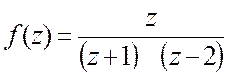 
9. State First shifting property of Laplace transforms.
10. If f(t) is a periodic function with period P, what is L {f(t)}.
PART B (5 x 12 = 60)
Answer All the Questions
11. (a)
Differentiate: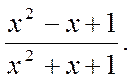 
(7)
(b)
Differentiate :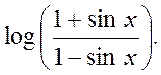 
(5)
(or)
12. (a)
If x = a cos q; y = b sinq; find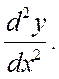 
(5)
(b)
If u = cos-1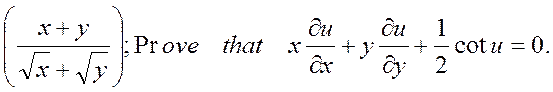 
(7)
13. (a)
Evaluate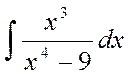 
(7)
(b)
Evaluate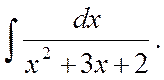 
(5)
(or)
14. (a)
Evaluate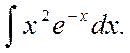 
(5)
(b)
Evaluate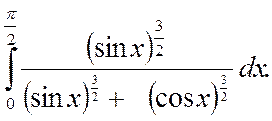 
(7)
15. (a) Prove that the real and imaginary parts of an analytic function satisfy the Laplace equation in two dimensions. (5)
(b) Prove that the function u = x3 3xy2 + 3x2 3y2 + 1 is Harmonic. Also find the conjugate Harmonic function n and the corresponding analytic function. (7)
(or)
16. (a) Find the image of the circle |z| = 2 under the transformation
w = z + 3 + 2i. (5)
(b) Find the bilinear transformation that maps the points 1 + i; -i; 2 i of the z-plane into the points 0, 1, I of the w-plane. (7)
17. (a) Evaluate:
where C is the
circle |z + 1 + i| = 2 using Cauchys Integral formula. (7)
(b)
Find the Laurrents series of f(z) =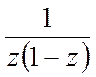 
in
the region
|z + 1| < 1. (5)
(or)
18. Evaluate
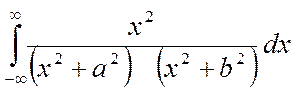using contour
integration.
19. (a)
Use laplace transform to evaluate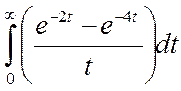 
. (7)
(b)
Find the inverse Laplace transform of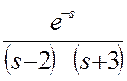 
. (5)
(or)
20. Solve y|| - 4y| + 8y = e2t; y(0) = 2; y|(0) = -2.
| Earning: Approval pending. |
