University of Hyderabad (UoH) 2008 M.Sc Statistics Entrance - Question Paper
Dopnrtment; of Mathematics and Statistics 11 n i versi ty of II y (i or a 1 >ac 1
Entrance <\\ainination - M.Sr. Statistics 7,00>
]lal 1 Ticket Number;
Time: 2 hours Max. Marks: 75
Part A: 25 marks Pari. 13: 50 marks
Instructions
1. Write your Booklet (VxIn mid Hall Ticket Number in (hr OMIl Answer S11(J' ? given to you. Also write the Hnil Ticket Number in tin; spac* provided above.
2. Then1 is negative marking. Do not. gamble.
3. Answers are l.o bo marked on the OiMK answer sheet, following the instructions provided (here upon.
1. Hand over the question paper booklet and the OMR answer sheet at the end of the examination.
5. Xo additional shoe's will be provided. 1-lough work can be done in the question paper ilsejf/ space provided al the end of the bookie!.
fi. Caleulators are. nol allowed.
7. '.[here are a total of 50 questions in par! A and 13 together.
8. The appropriate answer should be coloured in by either a blue or black ballpoint or sketch pen. DO NOT USE A PENCIL.
SECTION A
u-li question carries I mark fur a currect answer and O.iH uiiirks iur a u iun answer.
\
1. Lei .4 and tt be mutually exclusive (disjoint) events with strictly positive probabilities of occurrences. Then
(A) Ac and ft(:'are independent.
(B) Ac and Bc are mutually exclusive.
2. In a school there are 200 children born between 1st January 1999 and 30th June 1999 (end dates are included). The probability that no two children have the same birthday is
(B) 1
(C) 1
(D)555
3. if an event A occurs whenever event B occurs then ii is true l.lial.
(C) P(A) = P{B)
(D) P(A) = P(BC)
4. For the two events A and B} the probability of each event is at least 0.8. P(A P B) is in the interval
(A) [0, 0.3]
(B) (0.3, 0.5]
(C) [0.5, 0.6)
(D) [0.0, 0.8]
5. Suppose M is the mode and S2 the variance of n observations." If a negative constant a is added to all the observations, the mode and variance of these observations will be respectively
(A) M + a, S2
(B) M - a, S2 - a2
(C) M - a, S2
(D) M + a, .S2 l a2
Y\'0%
('*. Consider lh<' data: -2'\2. ().:{. -0.2N. -! .4. -0.0. -D. 0.1. u A n.J. \:>. -lt.fi. H)0\ I lie app|'Oprj;i! tin '.'lSUre nj (i'll! I'ai 1 <'i id; U H T ;!lllun; ( lie Ii liiuw'ili, is
3 . / }
J
0
>)
o
o
>)
>)
>)
o
o
3.
o j q
Q
Q
Q
(A) Ari1.11jiHl ir Mean (13) Geometric Mean
(C) Median
(D) Mode
7. IV>r a set of observations. (lie mean is 58, ilie median is 02 ;md the mode is 03. The data arc
(A) skewed If) the light (13) skewed In the l<Tt (0) symmetric about the median
(D) bimodal
8. Oni of 100 students in ;i class, 80 students got -10 marks in Maihemal ics and *20 got 50 marks. The mean. median, and mode of the marks in Mathematics for (his class arc respeclively
(A) 40, 40, 40 (13) 40, 40. 70
(C) 12, 40. 40
(D) 45. 40, 40
0. .V ~ /) thal is, (hr random variable A has mnlonn (or rectangu
lar) distribution in the interval ( 6, ii). For 0 <' n < fi, Iy( i\ < X < <\)
(B) f
') S3 0 |
10. Lot Xi ~ B(ni>p}), X2 ~ B(n2,p2)- Suppose px > p2 and E{X\) ~ ipfa), then
(A) E(X\) > E{Xl)
(B) E{X\) = HXl)
{0) E{X\) < E{Xl)
(D) E(X'l) and E(X) can not. be compared.
M-og-
11. A'i ami A-j <ire Poisson random variables wil.li inii'aiuclcis A] and A;, livrly. II /'(A'i > 0) /'(\2 . - 0), (.lieu
S
5
(A) MX-,) h'(A,)
' I >) ! '{Xi) X-t) >
(C) E(Xx) E(A\.j
(D) It is not possible lu sa.y any thin definitely.
12. The heights ul adult tuen arc: normally distributed wilii mean 1 .Oo nu.-ler* and si am lard deviation a meters. 30% of this population is of height less than Qn
I Ah meters. The percentage of adult men taller than 1.85 m is 4 |
(A) 25%
(B) 30% 1
C
(0) 40%
(D) 70%
13. Ar is a random variable with probability density function (pdf):
f.x(x) = exp{ :r2}. oo < x < oc.. Ol
v/r'
1 he mean and standard deviation of A are respectively
(A) 0 and
(B) 0 and ' |
(C) 0 and y/2 tj
(D) 1 and jry
14. The random variables X and Y are such that: X ( Y aud X Y arc positively correlated. Then
(A) Var(X + V) > Var(A' - Y)
(B) Var(X + V') < Var(X - y) w
(C) Var(A') < Var(y) 1
15. The correlation coefficient p{X,Y) between X and Y is Then p(U, K), where U = 2X 4- 7 and V = 3 V H- 8
(A) can not bo determined from the given information
(B) is 0
(D) is
Hi. A* is a random variable with P(X 1) ~ ~ and P(X - 0) Suppose. Y is a.uol.her random variable for which /(V'LY O') - 1000 mid E{Y\X ~ I) - 200,000 then E(Y)
..(A) can not be delermined from the jJven information (B) is TOH)
(() is 0
(D) is 101.1)
17. Two random variables A and )' an; uncorrelai.ed i!-
(A) \Vir(.V i V\) - V.u'i.V - V)
(1 \) V; 11 ( X Y) ----- V; i r | X) Ya r (Y)
(C) Var(A' - V) - Vm(.Y) - \ar(V)
(!)) Var(.Y) - Var(y)
18. The area nl' a circle inscribed in a square (Uial is all I hr sides of (.he square ;ire t.mif'rtits l.o Hie circle) whose side is chi is
(A) /i1 si | cm
(li) sq em
(C) ?rA sq cm (I.)) V sq cm
19. A and B two rn x n matrices, then
(A) Rank(A-i-B)Rank(A)~l-Haik (B)
(B) Rank(A | B)< min{Rank(A). Rank(B)}
(C) Rank(A-fB)> max{Rank(A), Rank(B)}
(D) None of the above.
20. A three digit number is obtained by drawing 3 numbers denoted by a, 6, c. from a purse containing 9 marbles numbered 1,2,...,9 with replacement,. The set. of all possible outcomes is
(A) {ate | {a,6,c} C {1,2,...,9}}
(B) {{a,(i,c} | {a,6,c} C {1,2,...,9}}
(C) {nbc | a {1,2,... ,9},/) 6 {1,2,...,9},c {1,2,. ..,9}}
(D){d5c j a <b < c, a e {1,2,....9},J> {l,2....,9}.r (1,2_____9}}.
\
J I. rite 11 u I ti I H'l' ol elements ill I he set ,V {({)./).....i |. !):/,<. {(*!},/
S , n i } i .
(l>)-''!i .
1C) 2"
(D) U2""1.
22. For testing a null hypothesis. the level a critical region is C\ il' (he: level of significance of the test, is reduced io (, the corresponding critical region
Ct
(A) contains C
(B) is conlaiiled in C
(C) is equal to C
(D) none of t he above can be said with certainilv.
23. Suppose you are told that there is a direct relationship between the price of a certain fruit and the amount of rainfall during the growing season. Ii ran be concluded that
(A) Price of the lruit, lends to be high when the rainfall is high.
(B) 1ricc of the fruit lends to be low when the rainfall is high.
(0) A large amount of rain causes price of the fruit to rise.
(1)) A lack of rainfall causes price of the fruit to rise.
i + -4-V
a J
24. The limit of the sequence W},, us n > oo where an
IS
(a) 0
(b)l
(d) none of the above
25. The negation of the statement5 Ash ok has read every book in the library is
(A) Ashok has not read any book in the library.
(B) Ashok has not read at least one book in the library.
(C) Ashok has read at most one book in the library.
(D) Ashok has read only one book in the library.
27. .All juTMtigejnnnt.s <>{ 11 h !l uumber:- I.....ms n>w ;i.re t -p m I Iv likelv
The probability tls;)( no two odd numbers ;ue rifxi (o curl; oIIkt is
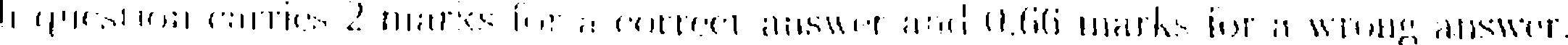 |
|
2G. ?Ml/t of the individuals in a. group ran spenk Knglisb and h'2% of I lie group an' females. The percentage of individuals urlio an; either English speaking or mule is al most, |
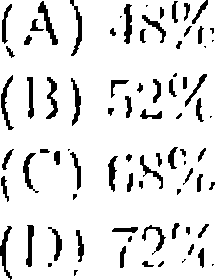
|
(A) 9 |
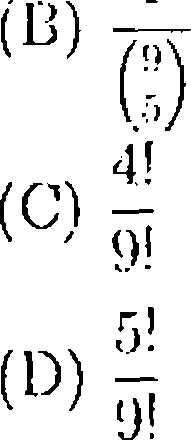 |
28. A and B are independent evenly with equal probabilities. If /)(/1U/i)
0.75, then
(A) P{A) - P{B) - 0.25
(B) - P(B) - 0.5
(C) P(A) - P(B) = 0.6
(D) P{A) P{B) 0.75
29. A packet of 5 shirts contains no defective or 1 defective shirt with probabilities 0.5 each. A dealer picks up a shirt from a packet at. random and rejects the packet if the selected shirt is defective, otherwise he accepts the packet. The probability that there is a defective shirt in an accepted packet is
30. There are 20 balls numbered 1.2.....20, two b;ilis each have lu In; placed
in 10 hew os. 11 every arrangemeni s.s equally likely, (hr: probability thal cac h box y,ois both balls with even numbers or both balls with udd numbers is
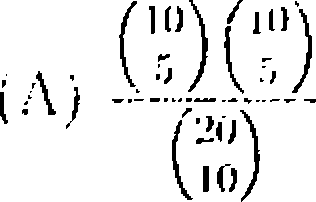
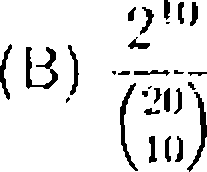
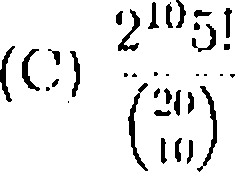
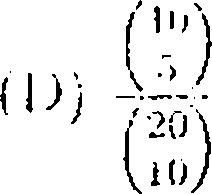
31. X ~ B(7,, let V - 7 - A'. then
(A) P{X ~ Y - -7) > P(X - K - 7)
(3) P{X - Y = -5) --- P{X - Y - 5)
(C) P(X - Y - -3) - ~Y ~ {)
(D) P(X-Y=Q) = \
32. Consider the quadratic equation x2 4- bx -r c = 0, obtained by selecting
a, 6 and c from the set {1, 2, 3} (a, 6 and c need not bo distinct). The
:{.'{ IiA) o.s. /(/>i-Vi uo, /(r 'i.-i f t />) n.ii.ilim /(,i h/Mkv) (A) is o.:r>2
o
o
N>
>)
>)
:i)
o
J
a
(Ii) is (.(MS
(C) is <).,X|
(I)) can not be del mui nod from the informat ion ivm.
31. Given below ;iit data on Y. A'| and X->
Y: 0.0 0.2 0.2 0.1 0.1 o.or, 0.0 J 0 A',: 2.01 2 2 2 2 2 2 2 A'o: 50 2 2 2 2 2 2 2
Lei. p, be the correlation coeflicioiil.- between )' and Aj. / 1,2. (.ben
(A) />j ()>
(B) px> f)2
(D) Pi - 0
35. Lei'. x.\ < .r-j < x:i be 3 real numbers and suppose we are given (.he values of X;\ X] and x\ x<). With this information we
(A) ean find the mean and the variance of .iq. j;2 ,.x;j
(B) ean not. find either the mean or the variance of.7q, x> . :r;{
(C) ean find I he mean bu! not the variance of x\. X2- x>
(D) ean Iiad the variance but not I,he mean of ./q. ra, .r:!
30. Jf A" is a Poisson random variable with mean 2. I lien f:'\X(X i)(A 2)j is
(A) 2 (13) 4
(D) 16
37. A random variable X follows Binomial(n, distribution. If P{X 4) P(X 5), then n is equal to
(A) 9

(B) 10 (G) 19
3
(D) 25
38. A random variable X has mean 5. If P{\X 5| > 5) -- 0.1. then the variance of X is
(A)/at most 1.5 (li) equal to I
.) equal lo 2 (I.)) at least 2.5
\
h-or
V2:c2(1 - a:). 0 < x '< I
(), otherwise
is 111
(A) (0, j;
10. The joint pdf of. two random variables X and Y is
exp{ - y J. 0 < :r < y < rx
1 (J, olnurvvi.se
The conditional pdf of A" iven i' --- y. f[x\ij) i.s
(A)
/(*W = 0, otherwise
(B)
othcne
(C)
,v , . ( exp{~5r}, x > 0
0, otherwise
(D)
f(r\v) = / sexpt-a:}, a- > 0 | 0, otherwise
'I I. The random variable A' follows exponential distribution with mean Thor i
(A) P(X < 2) > /'(.Y > 2)
(H) P(X < 2) < P(X > 2)
(D) P(X < 2) > P(Y > 0).
42. yVi, Aa is a random sample from the normo.1 population with mean /i and variance //2. Then unbiased estirnators for //. and fi2 respectively arc
(A)-Vr and
(B) mid S:*J.
(0) ,mr| X&&
IM. A hi!.-- |..If
J & 0':-r<.(P
v | 0, otherwise
where 0 yfc 0. Lei Ai,A2;. . ,Ao be a random sample from A'. The maxi-mtun likelihood estimator of 02 is
3 (\) X V", y
' ' 20
3
3
3
O
(B) EE. *?
((.') infixfyVf. X.%,.... Xj()} (0) maxjAj, A\>, ; A}.
44. XiX2* : An. n > 3 is a random sample from the normal distribution with moan 0 and variance a2, The best unbiased estimator for o" among (.he four given below is
--liu-,
(C)
45. Let X\, Xi, , Xn be a random sani[)Ie from the normal distribution with mean fi and variance 1. The most powerful lest for //> : ft ~ /t0 against. Hi : /i > //o is reject //o if for a suitable constant k
(A) X < k
(B) X > k (G) X 4 !
(I)) None of the above.
46. Let X is a Poisson distributed random variable with mean 2, then E(2X)
(A) does not exist
(B) is exp{2}
(C) is exp{4}
(D) is exp{G}.
47. There are 20 slips m a bag numbered 1.2., ,20. Three .slips are taken without replacement, the probability that the smallest of these three is at. most 7, the next smallest equal to 8 and the largest is at least 12 is
(A) strictly lass than ~
(B) at least ~ but less than ~
(C) fit If'iisl ~ but less thn
(D) al least
48. Given (.Ik; Linear Programming Problem maximize 8;/ | -s- t.r,; subject to
.T] -f- Qt,'2 b <j.7:| h 2:r,2 < 10 x [ ! 4j;2 < 4,
1 > 0, x2 > 0.
From lhe graphical roprc.vsentai.ion of these conditions the optimal solution is
(A) (2,0)'
(B) (1,3)
(C) (2,1/2)
(D) none of the above.
'10. The value of V' 23T | is
(13) 1
50. Let A = {x 6 3? : |.r 5j < 4} arid B ~ {.t 5!? : (xQ ~ 3x 4 2) > ()}. Then, A O B is
(A) empty
(B) an open interval
(C) a closed- interval
(D)4 a set, consisting of 2 points.
|
Attachment: |
| Earning: Approval pending. |
