University of Hyderabad (UoH) 2008 M.Phil NBHM RESEARCH ANF FELLO WHIP - Question Paper
NATIONAL BOARD FOR HIGHER MATHEMATICS
Research Scholarships Screening Test
Saturday, February 2, 2008
Time Allowed: Two Hours Maximum Marks: 40
Please read, carefully, the instructions on the following page
Please ensure that this booklet contains 9 numbered (and printed) pages. The back of each printed page is blank and can be used for rough work.
There are five sections, containing ten questions each, entitled Algebra, Analysis, Topology, Applied Mathematics and Miscellaneous. Answer as many questions as possible. The assessment of the paper will be based on the best four sections. Each question carries one point and the maximum possible score is forty.
Answer each question, as directed, in the space provided in the answer booklet, which is being supplied separately. This question paper is meant to be retained by you and so do not answer questions on it.
In certain questions you are required to pick out the qualifying statement) from multiple choices. None of the statements, or more than one statement may qualify. Write none if none of the statements qualify, or list the labels of all the qualifying statements (amongst (a), (b), and (c)).
Points will be awarded in the above questions only if all the correct choices are made. There will be no partial credit.
N denotes the set of natural numbers, Z - the integers, Q - the rationals, R - the reals and C - the field of complex numbers. Rn denotes the n-dimensional Euclidean space, which is assumed to be endowed with its usual topology. The symbol Zn will denote the ring of integers modulo n. The symbol ]a, b[ will stand for the open interval {x E R | a < x < b} while [a, b] will stand for the corresponding closed interval; [a, b[ and ]a, b] will stand for the corresponding left-closed-right-open and left-open-right-closed intervals respectively. The symbol I will denote the identity matrix of appropriate order. The space of continuous real valued functions on an interval [a, b] is denoted by C [a, b] and is endowed with its usual sup norm. The space of continuously differentiable real valued functions on [a,b] is denoted by C*[a, b] and its usual norm is the maximum of the sup-norms of the function and its derivative.
1.1 Let S7 denote the group of permutations of 7 symbols. Find the order of the permutation:
/1234567\
64573 1 2;
1.2 Write down the number of mutually nonisomorphic abelian groups of order 195.
1.3 For two ideals I and J in a commutative ring R, define I : J = {a E R : a J Clj. In the ring Z of all integers, if I = 12Z and J = 8Z, find I: J.
1.4 Let P be a prime ideal in a commutative ring R and let S = R\P, i.e. the complement of P in R. Pick out the true statements:
(a) S is closed under addition.
(b) S is closed under multiplication.
(c) S is closed under addition and multiplication.
1.5 Let p be a prime and consider the field Zp. List the primes for which the following system of linear equations DOES NOT have a solution in Zp:
5x + 3y = 4 3x + 6y = 1.
1.6 Let A be a 227 x 227 matrix with entries in Z227, such that all its eigenvalues are distinct. Write down its trace.
1.7 Let B be a nilpotent n x n matrix with complex entries. Set A = B I. Write down the determinant of A.
1.8 Let x and y be two non-zero n x 1 vectors. If yT denotes the transpose of y, what are the eigenvalues of the n x n matrix xyT ?
1.9 Let A be a real symmetric n x n matrix whose only eigenvalues are 0 and 1. Let the dimension of the null space of A I be m. Pick out the true statements:
(a) The characteristic polynomial of A is (A 1)mm-ra.
(b) Ak = Afc+1 for all positive integers k.
(c) The rank of A is m.
1.10 What is the dimension of the space of all n x n matrices with real entries which are such that the sum of the entries in the first row and the sum of the diagonal entries are both zero?
2.1 Let f (x) = 1+1x2 Consider its Taylor expansion about a point a E R, given by f (x) = =0 an(x a)n. What is the radius of convergence of this series?
2.2 Consider the series
n= 1
Pick out the true statements:
(a) The series converges for all real values of x.
(b) The series converges uniformly on R.
(c) The series does not converge absolutely for any real value of x.
2.3 Let f : R R be a continuous function. Which of the following imply that it is uniformly continuous?
(a) f is 2n-periodic.
(b) f is differentiable and its derivative is bounded on R.
(c) f is absolutely continuous.
2.4 Let f : [1,1] R be continuous. Assume that f_1 f (t) dt = 1. Evaluate:
lim f (t) cos2 nt dt.
n
2.5 Let f be a continuously differentiable 2n-periodic real valued function on the real line. Let an = f (t) cos nt dt where n is a non-negative integer. Pick out the true statements:
(a) The derivative of f is also a 2n-periodic function.
(b) |an| < Cn for all n, where C > 0 is a constant independent of n.
(c) an 0, as n to.
2.6 Let fn and f be continuous functions on an interval [a, b] and assume that fn f uniformly on [a, b]. Pick out the true statements:
(a) If fn are all Riemann integrable, then f is Riemann integrable.
(b) If fn are all continuously differentiable, then f is continuously differentiable.
(c) If xn x in [a, b], then fn(xn) f (x).
2.7 Let f : R R be a continuously differentiable function such that f '(0) = 0. Define, for x and y G R,
g(x,y) = f (Vx2 + y2).
Pick out the true statements:
(a) g is a differentiable function on R2.
(b) g is a differentiable function on R2 if, and only if, f (0) = 0.
(c) g is differentiable only on R2\{(0,0)}.
2.8 Find the square roots of the complex number 1 + 2i.
2.9 Evaluate:
f dz
J\z\=l (2 - z)z
the circle {|z| = 1} being described in the anticlockwise direction.
2.10 Pick out the true statements:
(a) There exists an analytic function f on C such that f (2i) = 0, f (0) = 2i and |f (z)| < 2 for all z G C.
(b) There exists an analytic function f in the open unit disc {z G C : |z| < 1} such that f (2) = 1 and f () = 0 for all integers n > 2.
(c) There exists an analytic function f on C whose real part is given by u(x, y) = x2 + y2, where z = x + iy.
3.1 Which of the following define a metric on R?
(a)
At 1 |x|-M 1
dl(x'y) = 1 + | x | . | y |
d2(x,y) = V1 x - y 1
(c)
d3(x,y) = 1 /(x) - /(y) 1
where / : R R is a strictly monotonically increasing function.
3.2 Let X and Y be topological spaces and let / : X Y be a continuous bijection. Under which of the following conditions will / be a homeomor-phism?
(a) X and Y are complete metric spaces.
(b) X and Y are Banach spaces and / is linear.
(c) X is a compact topological space and Y is Hausdorff.
3.3 Let (X, d) be a compact metric space and let {/a : a E A} be a uniformly bounded and equicontinuous family of functions on X. Define
/ (x) = sup /(x).
aG A
Pick out the true statements:
(a) For any t E R, the set {x E X : /(x) < t} is an open set in X.
(b) The function / is continuous.
(c) Every sequence {/an} contained in the above family admits a uniformly convergent subsequence.
3.4 Let D = {x E R2 : |x| < 1} where |x| is the usual euclidean norm of the vector x. Let / : D X be a continuous function into a topological space X. Pick out the cases below when / will NEVER be onto.
3.5 Let M(R) denote the set of all n x n matrices with real entries, consid-
2
ered as the space Rn . Which of the following subsets are compact?
(a) The set of all invertible matrices.
(b) The set of all orthogonal matrices.
(c) The set of all matrices whose trace is zero.
3.6 With the notations as in the preceding question, which of the following sets are connected?
(a) The set of all invertible matrices.
(b) The set of all orthogonal matrices.
(c) The set of all matrices whose trace is zero.
3.7 Let f : R R be a continuous function. Define
G = {(x,f (x)) : x E R} C R2.
Pick out the true statements:
(a) G is closed in R2.
(b) G is open in R2.
(c) G is connected in R2.
3.8 Let X be a topological space and let A C X. Let dA denote the boundary of A, i.e. the set of points in the closure of A which are not in the interior of A. A closed set is nowhere dense if its interior is the empty set. Pick out the true statements:
(a) If A is open, then dA is nowhere dense.
(b) If A is closed, then dA is nowhere dense.
(c) If A is any subset, then dA is always nowhere dense.
3.9 Let V be a complete normed linear space and let B be a basis for V as a vector space. Pick ot the true statements:
(a) B can be a finite set.
(b) B can be a countably infinite set.
(c) If B is infinite, then it must be an uncountable set.
3.10 Let V = C[0,1] with the metric
Let V2 = C [0,1] with the metric
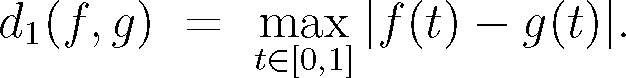
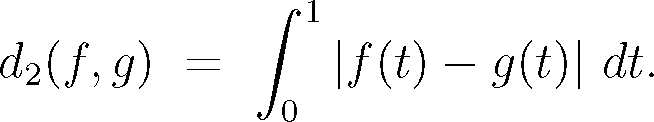
Let id denote the identity map on C[0,1]. Pick out the true statements:
(a) id : Vi V2 is continuous.
(b) id : V2 V1 is continuous.
(c) id : V1 V2 is a homeomorphism.
Section 4: Applied Mathematics
4.1 Write down the Laplace transform of the function f (x) = cos2x.
4.2 Let B denote the unit ball in RN, N > 2. Let aN be its (N-dimensional) volume and let flN be its ((N 1)-dimensional) surface measure. Apply Gauss divergence theorem to the vector field v(x) = x and derive the relation connecting aN and flN.
4.3 Assume that the rate at which a body cools is proportional to the difference in temperature between the body and its surroundings. A body is heated to 110C and is placed in air at 10C. After one hour, its temperature is 60C. At what time will its temperature reach 30C?
4.4 A body of mass m falls under gravity and is retarded by a force proportional to its velocity. Write down the differential equation satisfied by the velocity v(t) at time t.
4.5 Solve the above equation given that the velocity is zero at time t = 0.
4.6 Write down the critical points of the nonlinear system of differential equations:
f = y(x2 + 1) dt = 2xy2.
4.7 Classify the following differential operator as elliptic, hyperbolic or parabolic:
d 2 u d 2u d 2u U dx2 dxdy + Sy2.
4.8 Let B be the unit ball in the plane and let u be a solution of the boundary value problem:
Au = C in B du = 1 on dB
on
where A denotes the Laplace operator, SB denotes the boundary of B and In denotes the outer normal derivative on the boundary. Evaluate C, given that it is a constant.
4.9 Write down the dual of the linear programming problem:
Max. : 2x + 3y
such that
x + 2y = 3 2x + y > 4 x + y < 5 x > 0 , y > 0.
4.10 Write down the Newton-Raphson iteration scheme to find the square root of a > 0, by solving the equation x2 = a.
ra
2
f (t) = e x dx, (a > 0).
J-t2
5.2 Sum the series:
1 1 + 3 1 + 3 + 32
5.3 Sum the series:
11 11 11
1+34 + 542 + 743 +
5.4 Let A be the point (0,1) and B the point (2, 2) in the plane. Consider all paths made up of the two line segments AC and CB as the point C varies on the x-axis. Find the coordinates of C for which the corresponding path has the shortest length.
5.5 Find the area of the pentagon formed in the plane with the fifth roots of unity as its vertices.
5.6 Let A, B, C, D and E be five points marked, in clockwise order, on the unit circle in the plane (with centre at origin). Let a and ft be real numbers and set f (P) = ax + fty where P is a point whose coordinates are (x,y). Assume that f (A) = 10, f (B) = 5, f (C) = 4 and f (D) = 10. Which of the following are impossible?
(a) f (E) = 2
(b) f (E) = 4
(c) f(E) = 5
5.7 Let r identical red balls and b identical black balls be arranged in a row. Write down the number of arrangements for which the last ball is black.
5.8 It is known that a family has two children.
(a) If it is known that one of the children is a girl, what is the probability that the other child is also a girl?
(b) If it is known that the elder child is a girl, what is the probability that the younger child is also a girl?
5.9 A real number is called algebraic if it occurs as the root of a polynomial with integer coefficients. Otherwise it is said to be a transcendental number. Consider the interval [0,1] considered as a probability space when it is provided with the Lebesgue measure. What is the probability that a number chosen at random in [0,1] is transcendental?
5.10 List all primes p < 13 such that p divides n13 n for every integer n.
9
|
Attachment: |
| Earning: Approval pending. |
