University of Hyderabad (UoH) 2010 B.Sc Mathematics M.Sc Entrance - Question Paper
Entrance Examination : M.Sc. Mathematics, 2010
Hall Ticket Number
Part A : 25 marks Part B : 50 marks
Time : 2 hours Max. Marks. 75
Instructions
1. Write your Hall Ticket Number in the OMR Answer Sheet given to you. Also write the Hall Ticket Number in the space provided above.
2. There is negative marking. Do not gamble.
3. Answers are to be marked on the OMR answer sheet following the instructions provided there upon.
4. Hand over the question paper booklet and the OMR answer sheet at the end of the examination.
5. No additional sheets will be provided. Rough work can be done in the question paper itself/space provided at the end of the booklet.
6. Calculators are not allowed.
7. There are a total of 50 questions in Part A and Part B together.
8. The appropriate answer should be coloured in either a blue or black ball point or sketch pen. DO NOT USE A PENCIL.
Part-A
Each question carries 1 mark. 0:33 marks will be deducted for each wrong answer. There will be no penalty if the question is left unanswered.
The set of real numbers is denoted by R, the set of complex numbers by C, the set of rational numbers by Q, the set of integers by Z, and the set of natural numbers by N.
1. Let f(x) = cos ]x| and g(x) = sin |x| then
(A.) both / and g are even functions.
(B.) both / and g are odd functions.
(C.) / is an even function and g is an odd function.
(D.) / is an odd function and g is an even function.
2. The sequence j(-l)n 1 + - j is
(A.) bounded below but not bounded above.
(B.) bounded above but not bounded below.
(C.) bounded.
(D.) not bounded.
3.
x, xO, , .
x = o then / (0) is
(A.) 0.
(B.) 1.
(C.) 1/2
(D.) none of these.
be a matrix with integer entries such that 60.
a b c d 4-1% = 0 then
4. Let A If A2 + A
(A.) a2 a be = 1.
(B.) a2 a bd = 1.
(C.) o? a be = 1.
(D.) a2 + a be = 1.
5. The number of points at which the function
f(x) KM ~ 3) sin(7ra:)| + |(x2 l)(x3 27)| takes zero value is
(A.) 1.
(B.) 2.
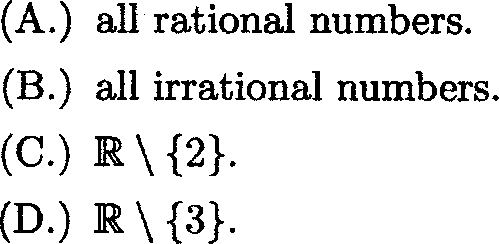
7. Consider the system of equations AX = 0, BX = 0 where A and
(C.) 3. (D.) 4.
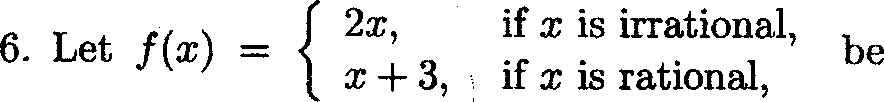 |
|
from R to R. Then the discontinuities of / are |
be a function defined
B are n x n matrices and I is an x 1 matrix. Which of the
following statements are true.
(i) det(A) = det(B) implies that the two systems have the same solutions.
(ii) The two systems have the same solutions implies det(yl) = det (B).
(iii) det(A) = 0 det(B) implies that the two systems can have different solutions.
(A.) All axe true.
(B.) (i) is true.
(C.) (iii) is true.
(D.) (i) and (ii) are true.
(x + 1) exp(x)
I
dx is equal to
8.
cos2 (xexp(x))
(A.) cot(x exp(x)) + C.
(B.) tan(x exp(a:)) + C.
(C.) log(sec(a;exp(x))) + C.
(D.) csc(xexp(a;)) + C.
9. If /(x) = x3 2x2 in (0,5) then the value of c to satisfy the Mean Value theorem is
(A.) 2. (B.) 3. (C.) 4.
(D.) None of these.
10. A random variable X takes the values 1,0 and 1 with probabilities 1/3 each. Then the mean value of X is
(A.) 0.
(B.) 1.
(C.) 0.5 (D.) 0.25.
11. Two numbers are drawn without replacement from 1,2, ,10. The probability that their sum is an even number strictly lies in
(A.) (0,1/3],
(B.) (1/3,1/2].
(C.) (1/2,3/4].
(D.) (3/4,1].
10 \/2x + 3 1 .
12. lim -........is equal to
xl y/5 + x-2
(A.) 4.
(B.) 3.
(C.) 2.
(D.) None of these.
13. For X, Y cR, define X+Y {x + y / x & X, y &Y}. An example where X + Y R is
(A.) x = q, y = R\Q.
(B.) X = Z,Y = [1/2,1/2].
(C.) X = (oo, 100], Y = {p G N/ p is prime}.
(D.) X = (-oo,100], y = Z.
14. Let / : [0,5] > R be continuous function with a maximum at x 2 then
(A.) the derivative of / at 2 may not exist.
(B.) the derivative of / at 2 must not exist and be nonzero.
(C.) the derivative of / at 2 must not exist and be zero.
(D.) the derivative of / at 2 can not exist.
15. The perimeter of the Caxdiod r = a(l + cos 0) is
(A.) 2a.
S-o
(B.) 4a.
(C.) 8a.
(D.) none of these.
16. If P(x) = x3 4- 7x2 + 6x + 5 then
(A.) P has no real root.
(H ) P has three real roots.
(C.) P has exactly one negative real root.
(D.) P has exactly two complex roots.
17. The number of diagonal 3x3 complex matrices A such that A3 = I is
(A.) 1.
(B.) 3.
(C.) 9.
(D.) 27.
18. The number of subgroups of order 4 in a cyclic group of order 12 is
(A.) 0.
(B.) 1. .
(C.) 2.
(D.) 3.
19. Let G be an abelian group and let /(*) = x2 be an automorphism of G if G is
(A.) finite.
(B.) finite cyclic.
(C.) prime order.
(D.) prime order > 7.
CO .
20. The series (
n=1 \Vn \/n + l
(A.) converges to 1.
(B.) converges to 1/2.
(C.) converges to 3/4.
(D.) does not converge.
21. The sequence 1 + i- j, js
I " )
(A.) unbounded and divergent.
(B.) bounded and divergent.
(C.) unbounded and convergent.
(D.) bounded and convergent.
1X
|l-z| x2, Ixl > 1
22. The function / :R-+R defined by /(x) = j
\x\ < 1,
(A.) continuous at all points.
(B.) not continuous at x = 1.
(C.) differentiable at all points.
(D.) none of the these.
23. Let T : R3 > R3 be the linear transformation defined by
T((xi,x2,23)) = + X2,X2 + x$,X3 + x{). Then an eigenvalue for T is
(A.) 0.
(B.) 1.
(C.) 2.
(D.) 3.
24. The solutions of x2y" + xy' + Ay = 0, x 0 are
(A.) cos(loga:), and sin(loga;).
(B.) cos(log:r), and sin(logai2).
(C.) cos(loga;2), and sin(loga;).
(D.) cos(21oga;), and sin(21oga;).
00 2n
25, The series n
-o
n\
(A.) converges in (-1,1). (B.) converges in [1,1]. (C.) converges in [1,1). (D.) converges in (-1,1],
Part-B
Each question carries 2 marks. 0.66 marks will be deducted for a wrong answer. There will be no penalty if a question is unanswered.
26. The integrating factor of the differential equation (y2 x2y)dx 4-x3dy = 0 is
(A.) (xy)'1.
(B.) (xy)~2.
(C.) xy.
(D.) xzyz.
27. An example of an infinite group in which every element has finite order is
(A.) non singular 2x2 matrices with integer entries.
(C.) the invertible elements in Z under multiplication.
(D.) the Quarternion group.
|
28. The value of the determinant (A.) 0. (B.) 1. (C.) 2. (D.) none of these. |
|
29. Three girls G\, G2, G3 and 3 boys B\, B2, 3 are made to sit in a row randomly. The probability that at least two girls are next to each other is
(A.) 0.
(B.) 1/10.
(C.) 1/20.
(D.) 9/10.
30. 3 red balls (all alike). 4 blue balls (all alike) and 3 green balls (all alike) are arranged in a row. Then the probabilitythat all 3 red balls are together is
(A.) 1/15.
(B.) 1/10!.
(C.) 8!/10!.
(D.) 3/10!.
31. The equation \x 1| + |z| + |x + 1| = x + 2, x 6 R has
(A.) no solution.
(B.) only one solution.
(C.) only two solutions.
(D.) infinitely many solutions.
32. A natural number V is said to be petty if all its prime divisors are < y'n. A natural number is square free if the square of a prime can not divide it. Then
(A.) Every square free number is petty.
(B.) All even numbers axe petty.
(C.) There exists an infinite numbers which are pretty.
(D.) Square of a prime number is petty.
33. For the sequence | y/n + | of real numbers
(A.) the greatest lower bound and least upper bound exist.
(B.) the greatest lower bound exists but not least upper bound.
(C.) the least upper bound exists but not the greatest lower bound.
(D.) neither the greatest lower bound nor the least upper bound exist.
34. Let / : 1 - 1 be a differentiable function and consider the following
W !/(*) - f(y)I < 1, Vz, y e R with \x - y\ < 1.
s
(ii) \f(x)\ < 1, Va; e R.
Then we have
(A.) (i) implies (ii) but (ii) does not imply (i).
(B.) (ii) implies (i) but (i) does not imply (ii).
(C.) (i) implies (ii) and (ii) implies (i).
(D.) (i) does not imply (ii) and (ii) does not imply (i).
35. Let U {(a, b,c,d) / a + b = c + d},V = {(a,b,c,d) / a = b, c = d} be subspaces of R4. Then the dimensions U and V are
(A.) 1 and 2 respectively.
(B.) 2 and 3 respectively.
(C.) 3 and 2 respectively.
(D.) 3 and 4 respectively.
36. Let / : [0,1] > R be continuous function and define g : [0,1] R
|
as g(x) = (f(x))2. Then |
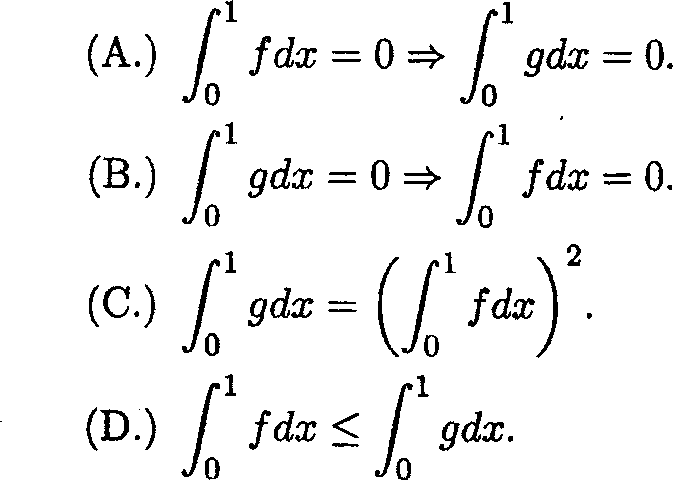 |
37. Let X be a set, {Aa / a 1} be a collection of subsets of X and
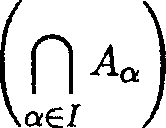
/ : X ->Xbea function. Then we have / =rvw
ael
if
(A.) X is finite.
(B.) I is finite.
(C.) / is one-one.
(D.) / is onto.
38. The value of the integral I log (\/l + x + \/l - x) dx is
(A.) log s/2-1.
(B.) 1 log \/2.
(C.) log\/2 + 1/2 + 7r/4.
(D.) log V2 - 1/2 + tt/4.
39. The derivative of the function y = sin 1
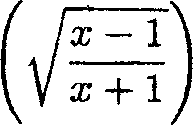
|
x 1 \ -- + sec | 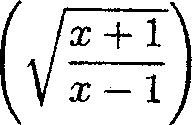 |
is
(A.) -1 (B.) 0. (C.) 1.
(D.) none of these.
40. Let T be the linear transformation defined bv T((xi,x2,x3,xi)) = c(xx - X2,X2 - xz,x$ X4). Then, which of the following statements are true?
(i) dimKer(T) = 1 if c 0.
(ii) dimKer(T) = 4 if c 0.
(iii) dimKer(T) = 1 if T is onto.
(A.) (i) and (ii).
(B.) (ii) alone.
(C.) (ii) and (iii).
(D.) (i), (ii), (iii).
41. Let Si and S2 be two series defined for x (1,1) as S\ =
00
OO
y(smn)xn and S2 = ]P(smn + cosn)xn then
71=0
(A.) Si and S2 are convergent.
(B.) Si and S2 axe bounded but axe not convergent.
(C.) Si is convergent.Si but S2 is only bounded.
(D.) Si and S2 are divergent.
then P is invertible and P 1 is equal to
3-3 3 2-3 4 0 -1 1
42. IfP =
(A.) (P2 + P + I)/3.
(B.) (P2 + P I)/3.
(C.) (P2-P + J)/3.
(D.) (P2 P /) /3.
43. Let (yn} be two convergent real sequences and let z~ = max{xn, yn} for each n e N. Then
(A.) {zn} is convergent.
(B.) {zn} is bounded but may not be convergent.
(C.) {zn} may not be convergent but {zn} has a convergent subsequence.
(D.) {zn} is convergent if and only if 3no G N 9 xn = ynVn > no.
44. The solution of the differential equation y7 y xy5 is
(A.) y = (x + cexp(-4x) + 1/4)4.
(B.) y = (x + cexp(4x) + l/4)~4.
(C.) y = (x + cexp(-4a;) +
(D.) y = (a; 4- cexp(4a;) -f 1/4)1/4.
45. Let / : 1 -> M be a continuous function such that f(n) = n, Vn Z. Then
(A.) / is identity.
(B.) |/(x)| < x, Vx R.
(C.) f(x) > 0, Vx (0, oo).
(D.) none of these.
46. Let {u, v, w} be a linearly independent set in the vector space R3 and let X = span{u,t; 4- w} and Y = span{tz;, u + u}. Then the the dimension of X f) Y is
(A.) 0.
(B.) 1.
(C.) 2.
(D.) can not be found from the information.
47. Let f(x) x\x\ and g(x) = sin|x| then
(A.) both / and g are differentiable functions.
(B.) f is differentiable function but g is not.
(C.) g is differentiable function but / is not.
(D.) both / and g are not differentiable functions.
48. Let u = x + ct, v = x ct and z = log u + sin v2 then is equal to
d2z 2 d2z dt2 dx2
(A.) -c.
(B.) -1.
(C.) -2c.
(D.) 0.
49. If a, 0 and 7 are the roots of the equation 15a:3 + 7x -the value of a3 + f33 + t3 is
11 = 0 then
(A.) 3/5.
(B.) 7/5.
(C.) 9/5.
(D.) 11/5.
50. Area of the region enclosed by the curves y = x2 x -is
2 and y 0
(A.) 7/2.
(B.) -7/2.
(C.) 9/2.
(D.) -9/2.
13
|
Attachment: |
| Earning: Approval pending. |
