Jawaharlal Nehru Technological University Anantapur 2008 B.Tech Supplimentary s, / ENGINEERING MECHANICS ( Common to Mechanical Engineering, Mechatronics, Metallurgy & Material Technology, Productio
SET-1
R07
JAWAHARLAL NEHRU TECHNOLOGICAL UNIVERSITY HYDERABAD
I B.TECH SUPPLEMENTARY EXAMINATIONS FEBRUARY - 2010 ENGINEERING MECHANICS (COMMON TO MMT & AE)
Time: 3hours Max.Marks:80
Answer any FIVE questions All questions carry equal marks
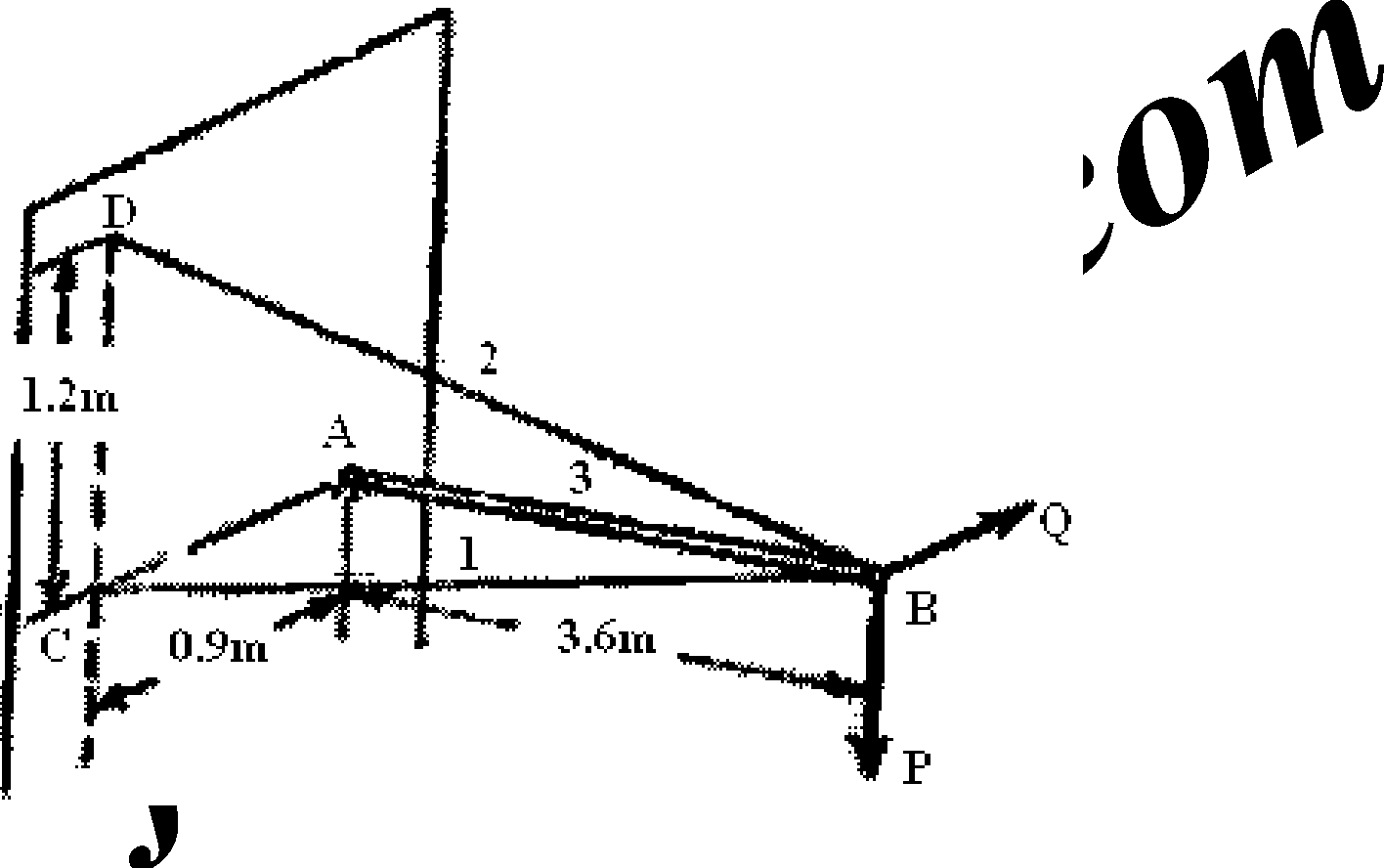
1. A strut AB attached to the face of a vertical wall at A by a spherical hinges stands perpendicular to the wall and is supported by two guy wires, as shown in Figure. At B, in a plane parallel to the wall, two forces P and Q acts as shown, Q being horizontal and P, vertical. Find the axial forces produced in the members if P = 500 N and Q= 1000 N. [16]
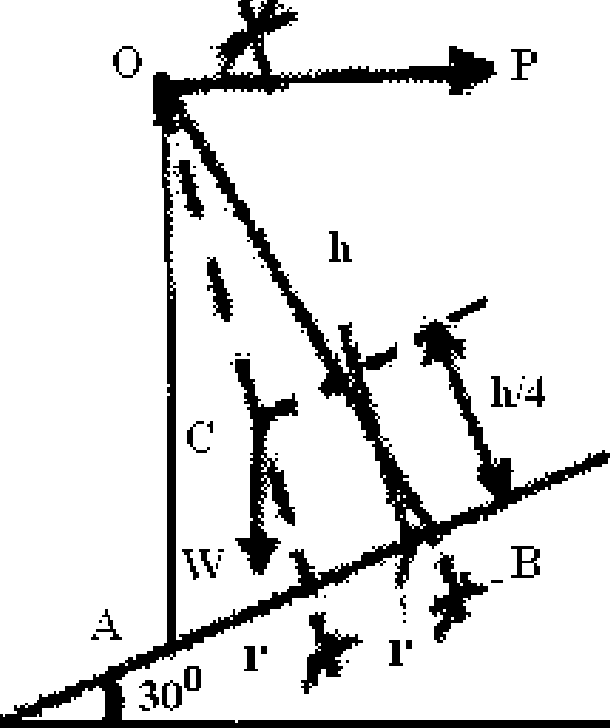
;ht circular cone of altitude h = 305 mm and radius of base r = 75 mm fils rts center of gravity 'C on its geometric axis at the distance h/4 above the base. This cone rests on an inclined plane AB, which makes an angle of 300 with the horizontal and for which the coefficient of friction is n = 0.5.A horizontal force 'P is applied to the Vertex 'O of the cone of the figure as shown. Find the maximum and minimum values of P consistent with equilibrium of the cone. If the weight W = 405 N. [8+8]
b) What must be the angles between the plane faces of a steel wedge used for splitting logs if there is to be no danger of the wedge slipping out after each blow of the sledge?
3.a) State laws of friction.
b) An open belt of width 80 mm connects a pulley of diameter 600 mm on the secondary shaft to a pulley of diameter 400 mm on the machine shaft. The shafts are three meters apart. The secondary shafts has a speed of 100 r.p.m. Find the maximum permissible stress in the belt if the safe working tension is 15N/mm width and ju = 0.3. [8+8]
4.a) State and prove parallel axis theorem.
b) Find the centroid of the shaded lamina shown figure. [8+8]
5. A cylinder of diameter 500mm and height \200mm has mass density of 8000kg/m3. Find out the mass moment of inertia of the cylinder.
a) With respect to the axis of the cylinder and
b) About a line which coincides with an end face of the cylinder and passing through the centre of this face P\ [8+8]
A train is uniformly accelerated and passes successive kilometer stones with velocities of 18km/hr and 36km/hr respectively. Calculate the velocity when it passes the third kilometer stone. Also find the time taken for each of the two intervals of one kilometer.
6.a)
Aball projected vertically upwards attains a maximum height of 400 meters. Calculate the velocity of projection and compute the time of flight in air. At what altitude will this ball meet a second ball projected vertically upwards 4 seconds later with a speed of 120 meters per second? [8+8]
7.a) A body weighing 20N is projected up a 20 inclined plane with a velocity of 12m/s, coefficient of friction is 0.15. Find
i) The maximum distances S, that the body will move up the inclined plane.
ii) Velocity of the body when it returns to it original position.
b) Find the acceleration of the moving loads as shown in figure . Take mass of P = 120kg and that of Q = 80kg and coefficient of friction between surfaces of contact is 0.3. Also find the tension in the connecting string. [8+8]
8.a) What is a simple pendulum? Under what conditions its motion is regarded as simple harmonic.
b) A simple pendulum gain 4 seconds per day. Determine the change in length of the pendulum in order to correct the time. [8+8]
C
(r
SET-2
R07
JAWAHARLAL NEHRU TECHNOLOGICAL UNIVERSITY HYDERABAD
I B.TECH SUPPLEMENTARY EXAMINATIONS FEBRUARY - 2010 ENGINEERING MECHANICS (COMMON TO MMT & AE)
Time: 3hours Max.Marks:80
Answer any FIVE questions All questions carry equal marks
Find the reactions Ra and Rb induced at the supports A and B of the right-angle bar ABC supported as shown in figure and subjected to a vertical load P applied
1.
at the mid-point of AC.
|
[16] |
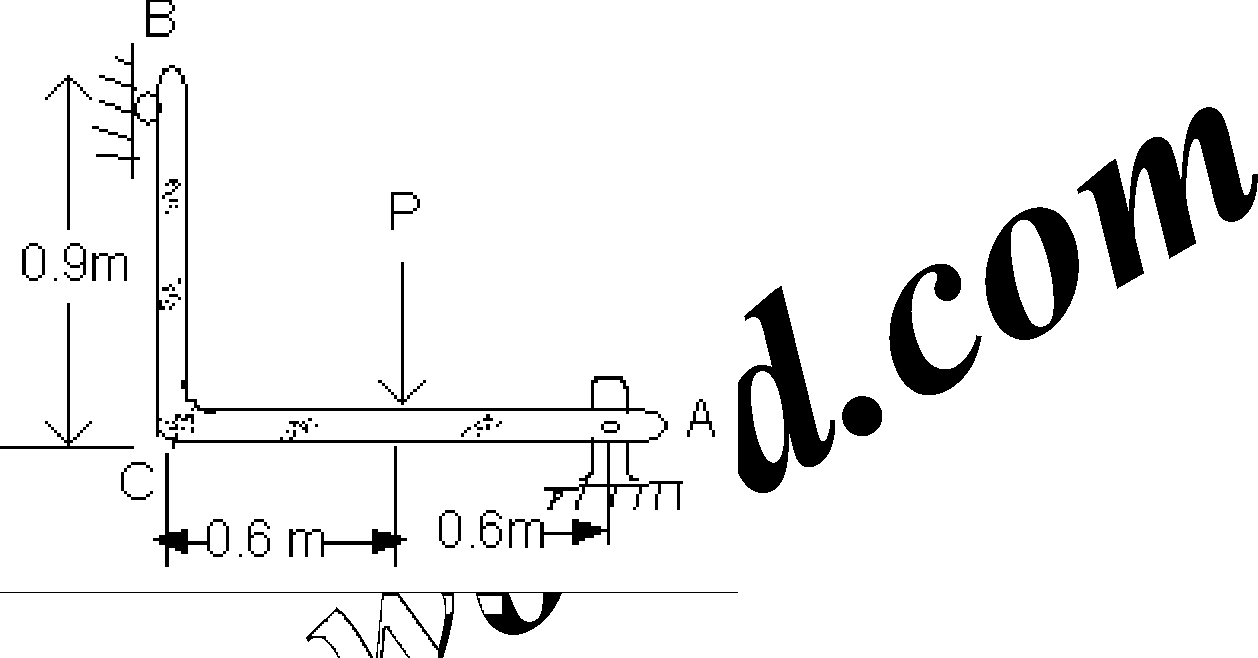 |
2.a)
in
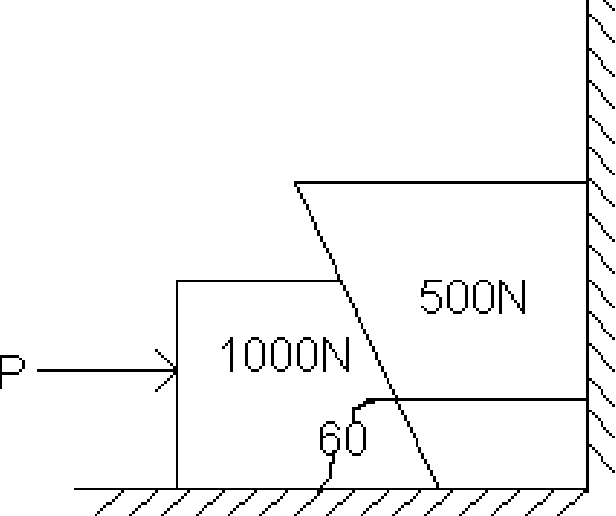
Referring to figure below the coefficjfem of the friction is as follows: 0.25 at the floor, 0.03 at the wall and 0.20 between blocks. Find the minimum values of a horizontal force P applied to the lower blocks that will hold the system equilibrium.
b) Two identical blocks A and B are connected by a rod and rest against vertical and horizontal planes respectively, as shown in figure. If sliding impends when# = 450, determine the coefficient of frictionu , assuming it to be the same at both floor and wall. [8+8]
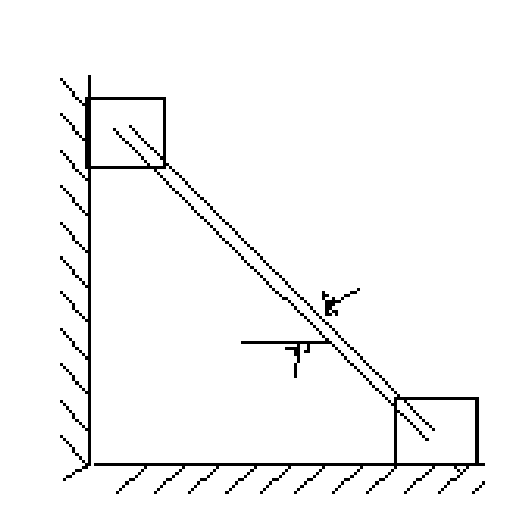
3.a) Derive an expression for length of a crossed belt in standard form. b) An engine drives a shaft by means of a belt. The driving pulley of the engine is 3 meters and that in the shaft 2 meters diameter. If the engine runs at 150 r.p.m. What will be the speed of the shaft when.
i) There is no slip.
ii) There is a slip of 3%? [8+8]
State and prove parallel axis theorem.
4.a)
b)
Find the moment of inertia about the horizontal centroidal axis of shaded portion.
_ [8+8]
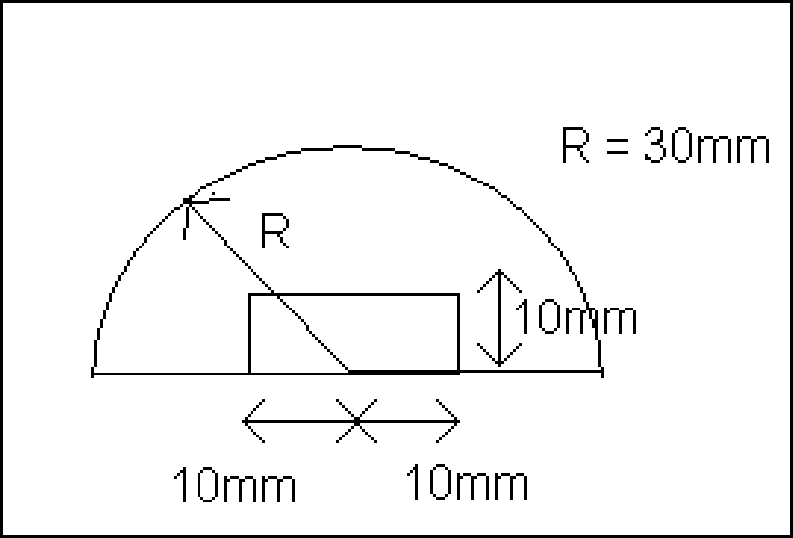
Show that the moment of inertia of a homogeneous triangular plate of weight W with respect to its base of width b is Wb2/6g where g is the acceleration due to gravity.
5.a)
b)
6.
A right circular cone has the radius of base as 200mm and height 500mm. The mass density of the cone is 7800kg/m3. Find out the mass moment of inertia of this cone about a line which passes through the vertex of the cone and which is parallel to the base of the cone. [8+8]
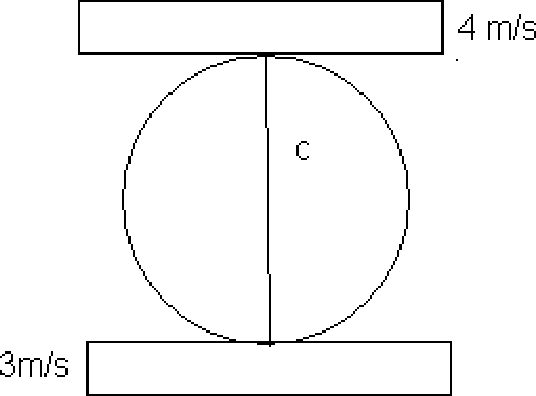
A roller of radius 0.1m rides between two horizontal bars moving in opposite directions as shown in figure. Assuming no slip at the points of contact A and B, ' cate the instantaneous center 1 of the roller. Also locate the instantaneous
loca
cen
tjr when both the bars are moving in the same directions.
[16]
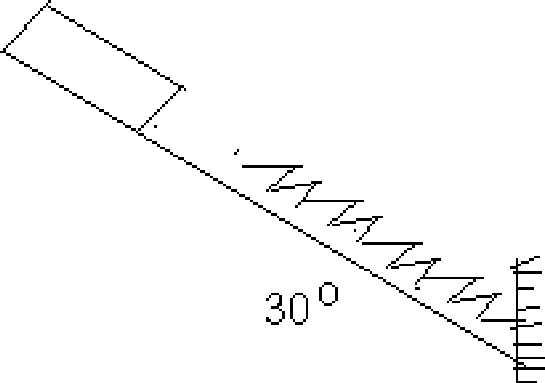
7.a) A homogeneous solid cylinder of weight 100 N whose axis is horizontal rotates about its axis, in frictions bearings under the action of the weight of a 10 N block which is carried by a rope wrapped around the cylinder. What will be angular velocity of cylinder two seconds after the motion starts? Assume the diameter of cylinder as 100cm.
b) A block of mass 5Kg resting on a 300 inclined plane is released. The block after traveling a distance of 0.5m along the inclined plane hits a spring of stiffness 15N/cm. Find the maximum compression of spring. Assume coefficient of friction between the block and the inclined plane is 0.2. [8+8]
A spindle of diameter 30mm and of length 3.5m carries a weight of 280N at one end. The other end of the spindle is fixed. The weight is pulled downwards and released so that the spindle is having free longitudinal vibrations. Neglecting the weight of the rod, determine the frequency of vibration. Take the moduluof elasticity of the material of the spindle as 2 x 1011 N / m2

SET-3
R07
JAWAHARLAL NEHRU TECHNOLOGICAL UNIVERSITY HYDERABAD
I B.TECH SUPPLEMENTARY EXAMINATIONS FEBRUARY - 2010 ENGINEERING MECHANICS (COMMON TO MMT & AE)
Time: 3hours Max.Marks:80
Answer any FIVE questions All questions carry equal marks
1.a) Define free body diagram, Transmissibility of a force and resultant of a force. b) Two identical rollers, each of weight 100 N, are supported by an inclined plane and a vertical wall as shown in Figure. Assuming smooth surfaces, find the reactions induced at the points of support A, B and C. [8+8]
\
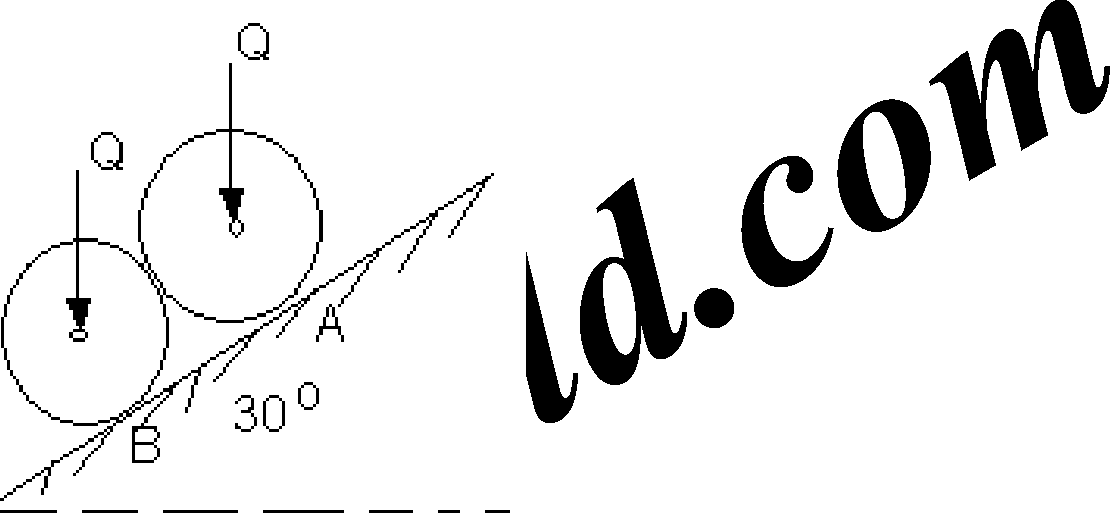
\
\
\
\
\
\
\
\
\
\
\
\
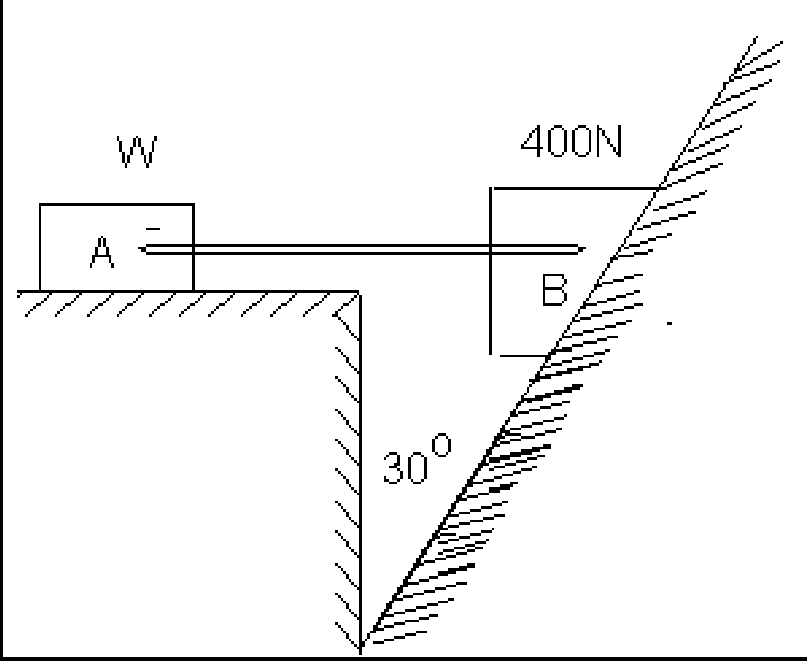
2.a) Two blocks, connected by a horizontal link AB are supported on two rough planes as shown in Figure. The coefficient for friction of block A on the horizontal plane isn = 0.4 . The angle of friction for block B on the inclined plane is# = 150.
What is the smallest weight W of block A for which equilibrium of the system can exist?
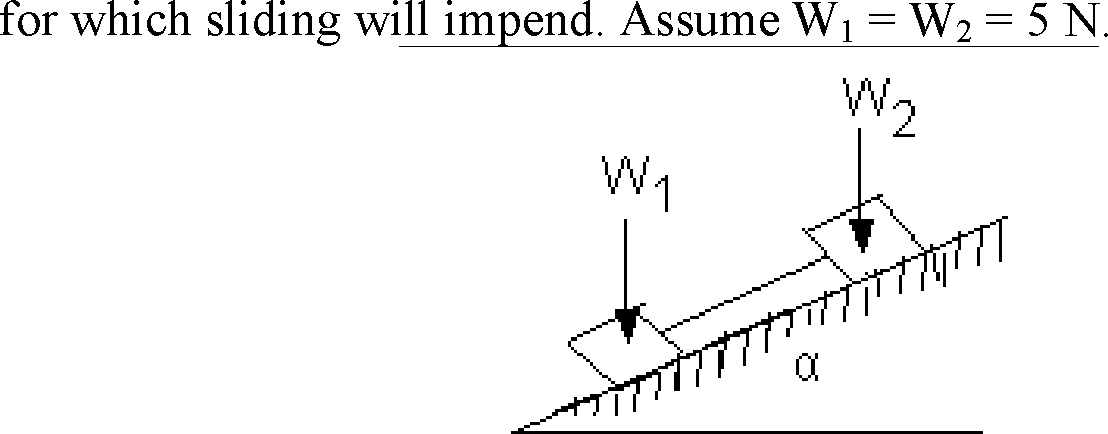
b) Two blocks of weight W1 and W2 rest on a rough inclined plane and are connected by a short piece of string in Figure below. If the coefficients of friction are /u1 = 0.2 and /u2 = 0.3, respectively, find the angle of inclination of the plane
What are the assumptions to be made to derive an expression for the limiting ratio of tension?
3.a)
b)
In flat belt, the initial tension is 1800N. The angle of lap on the smaller pulleys is 1700. The coefficient of friction between the belt and pulley surface is 0.25. Diameter of pulley is 900mm and it runs at 450 r.p.m. Determine the power that can be transmitted at the above speed. Neglect the effect of centrifugaltension.
|8+8]
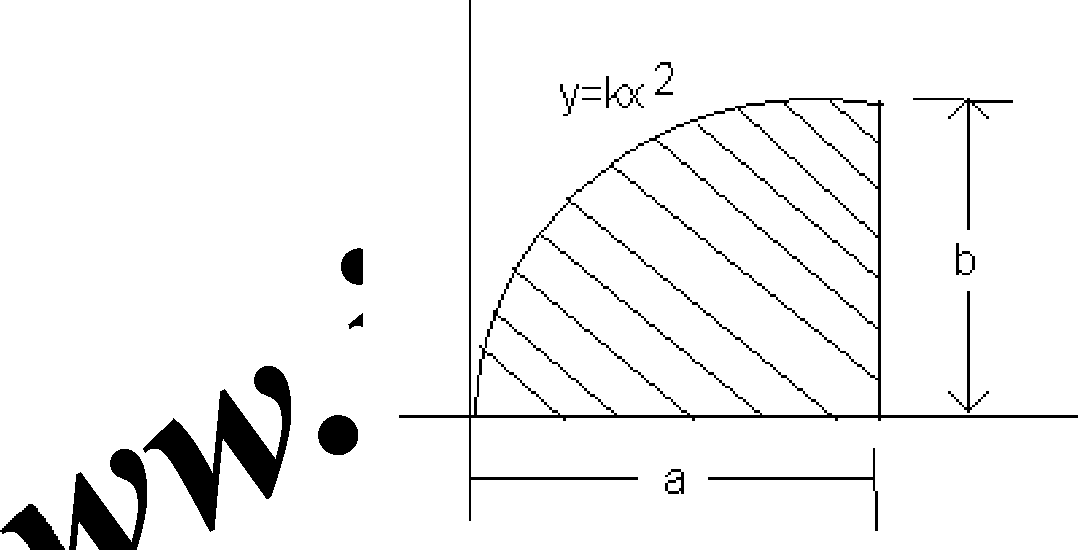
ie line x = a. as shown
|
Locate the centroid of given parabola bounded by X-axis in the Figure . v i |
 |
|
Locate the centroid of the wire bent as shown in Figure |
4.a)
iO
|
100 mm | 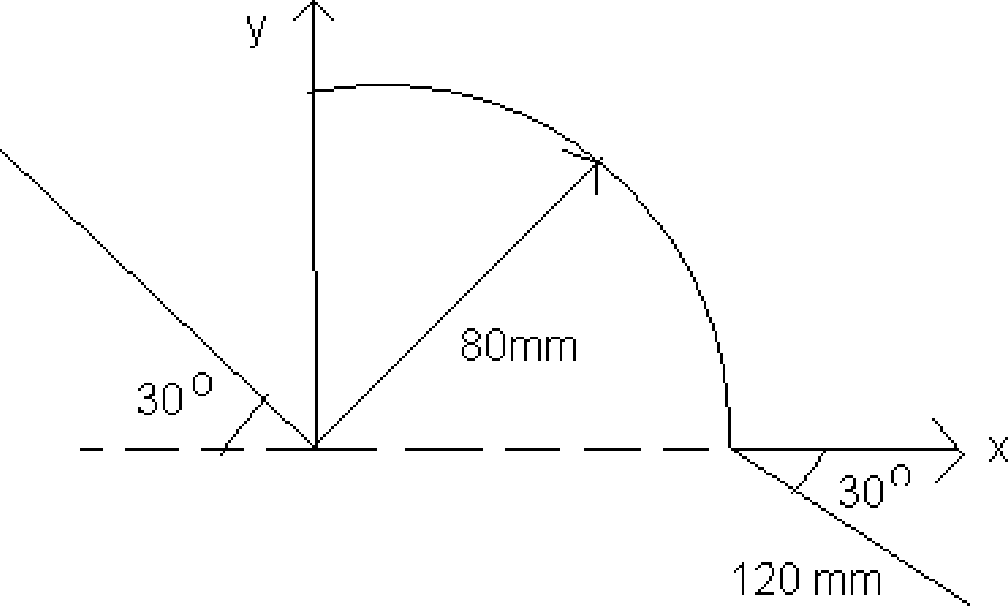 |
5.a) Determine mass moment of inertia of slender rod of length L about its centroidal axis normal to the rod. b) Derive the expression for mass moment of inertia of a cone of height 'h and base radius 'r and mass density 'w with respect to its geometric axis. [8+8]
6.a) A railway car is moving with a velocity of 20m/s. The diameter of the wheel is 1m. The wheel is running on a straight rail without slipping. Find the velocity of the point on the circumference at 600 in the clockwise direction from the top at any instant.
b) A 600mm diameter flywheel is brought uniformly from rest to a speed of 350rmp in 20 seconds. Determine the velocity and acceleration of a point on the rim 2 seconds after starting from rest. [8+8]
7.a) An automobile moving with a uniform velocity of 40Kmph is accelerated by increasing the traction force by 20%. If the resistance to motion is constant, find the distance traveled before it acquires 50Kmph. Use work-energy method.
b) A solid cylinder and a sphere are started tat the top of an inclined plane, at the same time, and both roll without slipping down the plane. If, when the sphere reaches the bottom of incline, the cylinder is 12m, what is the total length 'S of the incline? [8+8]
8. A vertical shaft 100mm in diameter and 1m in length has its end fixed to the ceiling. At the other end, it carries a disc of mass 500kg having a rac gyration of 450mm. The modulus of rigidity for the material of shaft Determine the frequency of torsional vibrations.

SET-4
R07
JAWAHARLAL NEHRU TECHNOLOGICAL UNIVERSITY HYDERABAD
I B.TECH SUPPLEMENTARY EXAMINATIONS FEBRUARY - 2010 ENGINEERING MECHANICS (COMMON TO MMT & AE)
Time: 3hours Max.Marks:80
Answer any FIVE questions All questions carry equal marks
Define resultant, coplanar concurrent force system.
1.a)
b)
A ball of weight W rests upon a smooth horizontal plane and has attached to its centre two strings AB and AC which pass over frictionless at B and C and carry loads, P and Q, respectively, as shown in Figure . If the string AB is horizontal, find the angle a that the string AC makes with the horizontal when the ball is in a position of equilibrium. Also find the pressure R between the ball and the plane.
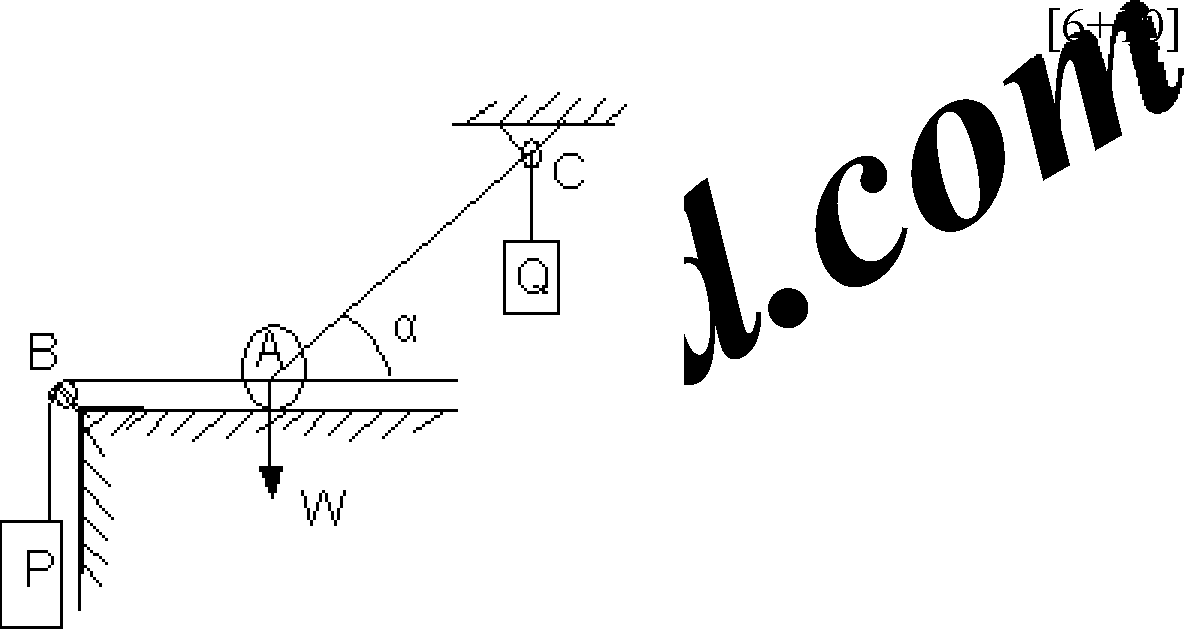
The ends of a heay prismatic bar AB are supported by a circular ring in a vertical plane as shown in figure. If the length of the bar is such that it subtends an angle of 900-ipi ring and the angles of friction at A and B are each, what is the test angle of inclination a that the bar can make with the horizontal in a mion of equilibrium.
2.a)
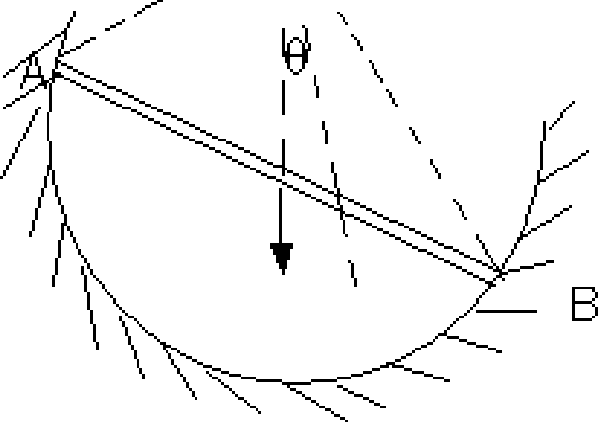
b) Determine the force P required to start the wedge shown in figure. The angle of friction for all surface contact is 15. [8+8]
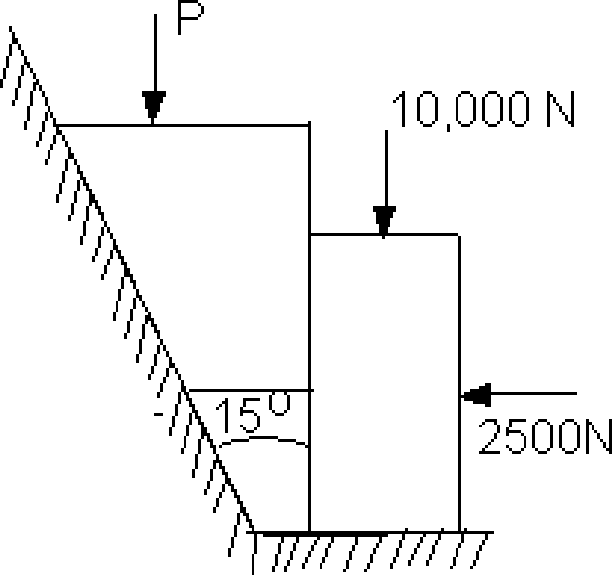
A belt transmits 15 KW from a pulley of 900 mm diameter running at 300 r.p.m. The angle of lap is 1600 and coefficient of friction is 0.25, thickness of the belt is 6 mm and its density is 1000 kg/m3. Determine minimum width required if stress in belt is limited to 2 N/mm2.
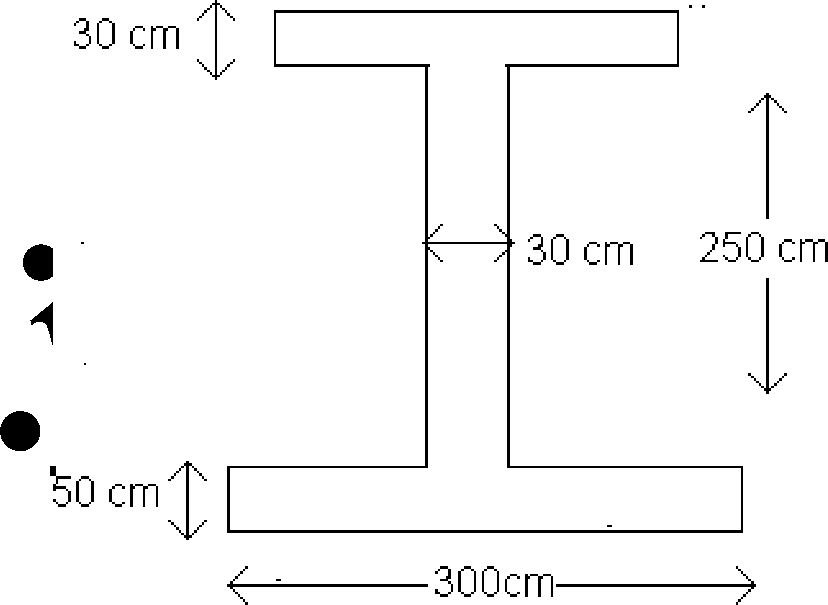
Find the moment of inertia about horizontal centroida? radius of gyration about the same axis. _
<-100 cm->
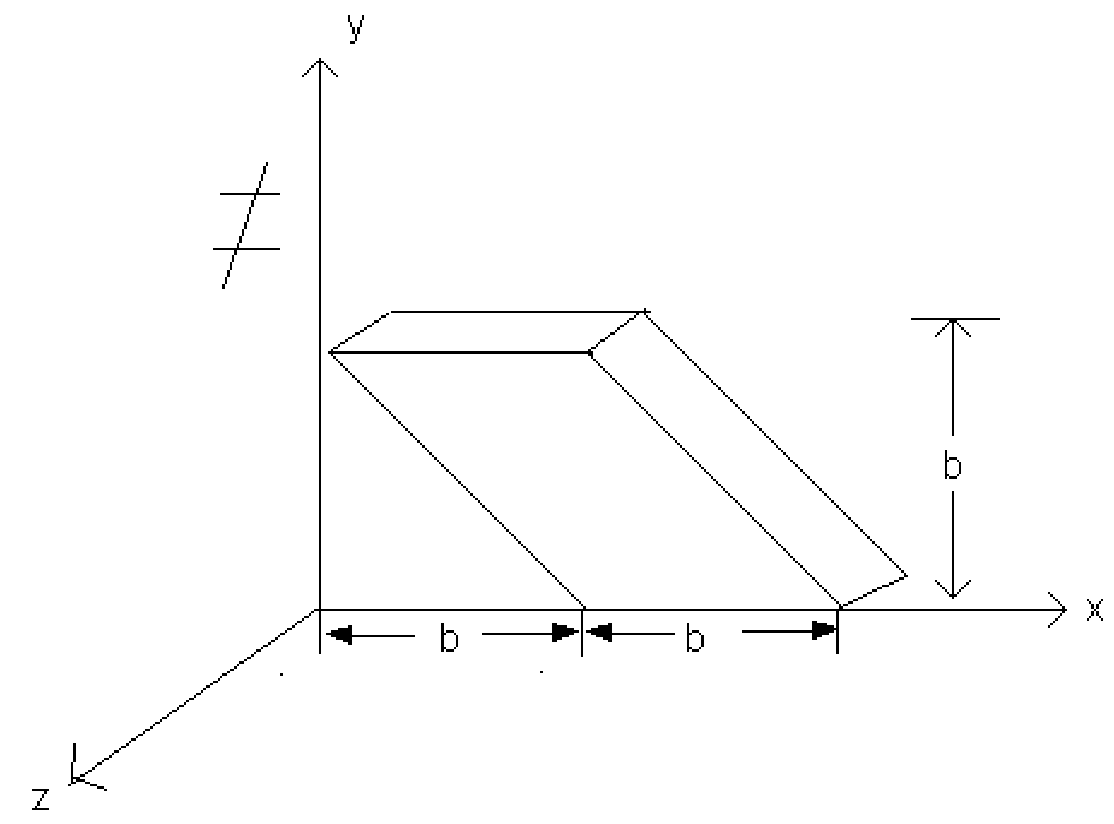
A thin plate of mass m is cut in the shape of parallelogram of thickness t as shown in fig. Determine the mass moment of inertia of the plate about the X- axis.
[16]
th of the belt
(U)W6]
and also find the [16]
dal ax
"A
xis
o
5.
6. In a engine system shown in Figure the crank AB has a constant angular velocity of 4000 r.p.m. For the crank position indicated, determine
i) Angular velocity of connecting rod BD.
ii) Velocity of piston P. [16]
' B '
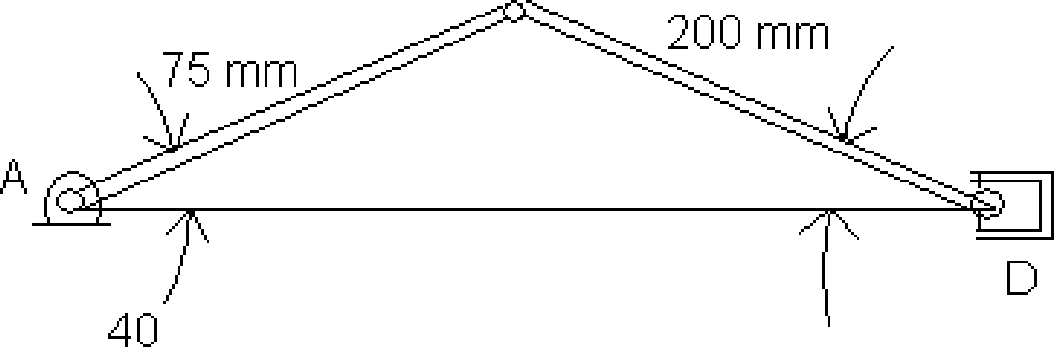
7.a) A homogeneous sphere of radius a = 100 mm and weight W = 100 N can rotate freely about a diameter. If it starts from rest and gains, with constant angular acceleration, an angular speed n = 180 rpm, in 12 revolutions, find the acting moment.
b) A block starts from A. If the coefficient of friction between all surfaces of contact is 0.3, find the distance at which the block stops on the horizontal plane. Assume the magnitude of velocity at the end of slope is same as that at the
beginning of the horizontal plane.
[8+8]
I*
|
A |
 |
Iprrngs of stiffness K1 and K2 are connected in series. Upper end of the iund spring is connected to a ceiling and lower end carries a load W. Find the equivalent spring stiffness of the system. If the above two springs are connected in parallel then find the equivalent spring stiffness of the system also.
prings prings o
cTowmop os
***** [16]
|
Attachment: |
| Earning: Approval pending. |
