Mahatma Gandhi University (MGU) 2011-1st Sem M.C.A Mathamatical foundation of computer science- - Question Paper

G 1183    (Pages : 3)

Reg. No. Name......

M.C.A. (AFFILIATED COLLEGES) DEGREE EXAMINATION, MARCH 2011

First Semester

MATHEMATICAL FOUNDATION OF COMPUTER SCIENCE

(2007 admission onwards)

Time : Three Hours    Maximum : 75 Marks

Answer any ten questions from Part A and all questions from Part B.

Part A

1.    If A and B are any two sets show that An(BuC) =(AnB) u(A n C).

2.    Prove that the relation Congruence modulo m given by R = {(x, y) \ x - y is divisible by mj over the set of positive integers is an equivalence relation.

3.    Let A = {l, 2,3,4}. p(A) be the power set of A and be the relation on the set p (A). Draw the Hasse diagram of (p(A), c).

4.    Let (L, <) be a lattice. For any a, b, c, eL prove that a * (> c) > (a * b) (a * c).

- 5. Define the following :

(i)    Finite automaton.

(ii)    Transition diagram.

(iii)    Regular language.

6.    Construct truth table for 1(Pv(QaR)) ((P v Q) a (P v R)).

7.    Show that (p~>q) Q ~p) is a tautology.

8.    Define adjacency matrix. Draw the graph corresponding to the adjacency matrix given below :

0 1-0011

0 110 10

0 0 0 1 0 1

1 0 0 0 0 0

10 0 10 0

* 9. Define a complete bipartite graph. Draw the complete bipartite graphs K_{2 3}, K_{2 4} and Kg ₅.

10. Show the binary search tree after inserting 3, 1, 4, 6, 9, 2, 5, 7 into an initially empty binary tree.

Turn over

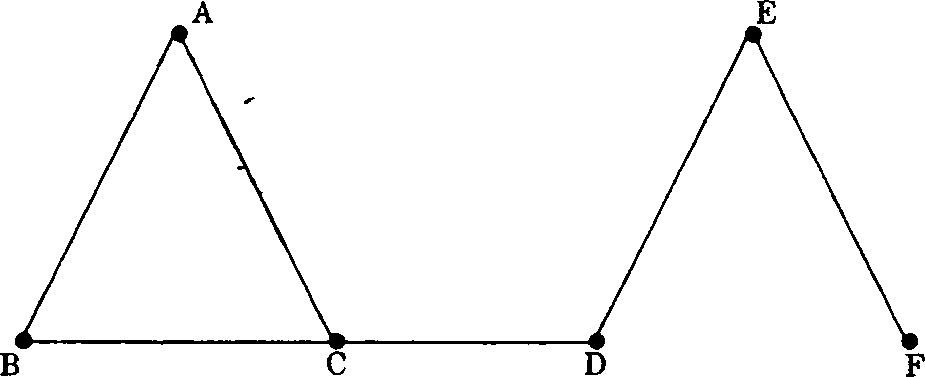
12. Prove that the complete graph K₄ is planar.

Part B

Answer all questions.

All questions carry equal marks.

13. (a) (i) If A, B, C are any three sets prove that A x(B n C) = (A x B) n (A x C).    (4 marks)

(ii) If R and S are equivalence relations on a set A, prove that RnS and RuS are equivalence relations of A.

(5 marks)

Or

11 Ira

(b) (i) Prove by mathematical induction that i 2 ⁺ 2 3 ⁺.....⁺ n(n +1) ~ n +1

/

(ii) Consider the functions f,g : R R defined by f (.r) = x² + 3* + 1, g(x) = 2x -3. Find the composition functions (i) fof ; (ii) fog ; (iii) gof; (iv) gog.

(5 marks)

14. (a) Show that the lattices given below are non-distributive :

i

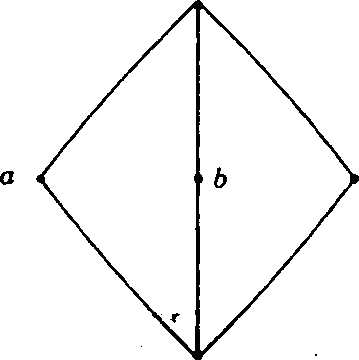
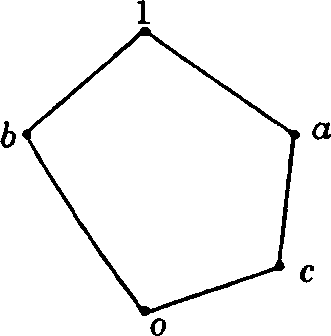
(9 marks)

Or

(b) Construct a deterministic finite automata accepting the set of all strings with three consecutive Os.

15.    (a) Show that (3.x) M(x) follows logically from the premises (x) (H(x) - M(x)) and (3x) H (x).

(9 marks)

Or

(b) Show that R a (P v Q) is a valid conclusion from the premises P v Q, Q R, P M and 7 M.

(9 marks)

16.    (a) Define the following (i) Hamiltonian path ; (ii) Hamiltonian circuit ; and (iii) Hamiltonian

graph. Show that the following graph is Hamiltonian. Find a Hamiltonian circuit for the graph.

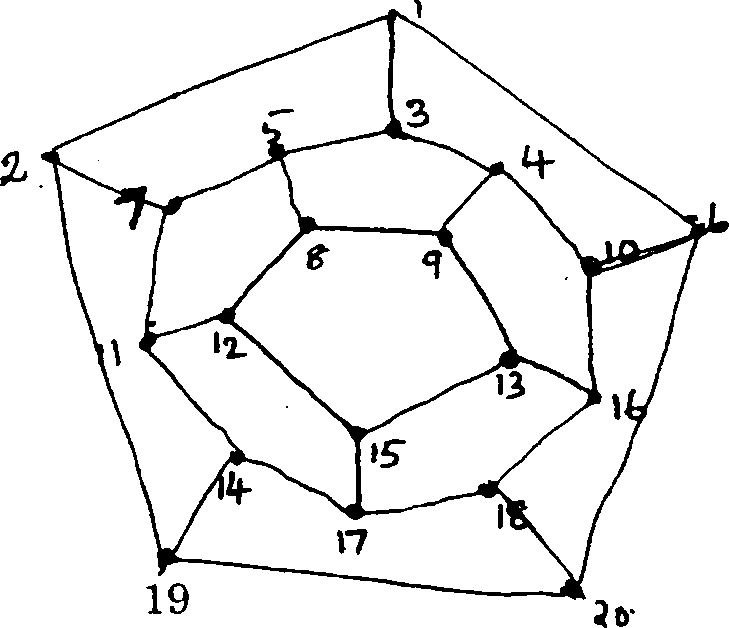
(9 marks)

Or

(b) A connected graph is an Euler graph if and only if itcan be decomposed into circuits.

17. (a) State and prove Eulers formula.

Or

(b) Find a minimum spanning tree for the graph with labelled edges in the given figure.

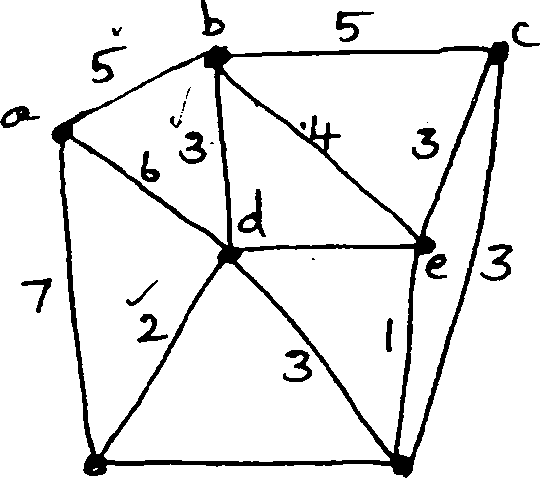
(9 marks) [5 x 9 = 45 marks]

Attachment: mahatma-gandhi-university--mgu--2011-m-c-a--34750-1.pdf

Earning:   Approval pending.