Aligarh Muslim University (AMU) 2010 B.Sc Physics Mathematical Methods - Question Paper
(4292)
2009-2010
B.Sc. (HONS.) (PART-III) EXAMINATION (PHYSICS)
MATHEMATICAL METHODS (PH - 307)
Maximum Marks : 40 Duration : Three Hours
NOTE: (i) Answer ALL questions.
(ii) Marks are indicated against each part.
1. (a) State and prove Cauchys integral theorem. (04)
(b) Assuming that f(z) is analytic on and within a closed contour c and that point Zo is (03) within c, show that:
rf'(z)dz r f'{z)dz ; z-*o l(z~Zo)2
l7. (a) Define an analytic function and obtain the Cauchy-Riemann differential equations. (04)
(b) Using Taylor expansion show that: (P3)
1 00 =yy i-t &
2. (a) State and prove Stokes theorem of vector analysis. Show that Greens theorem in the (04)
plane is the special case of Stokes theorem.
(b) Show that gradient of a differentiable scalar function f at a point P of surface S. (03) f(x,y,z)=constant, is a normal vector of S at P.
3. (a) Define Beta and Gamma functions and show that: (03)
f(n) ftm) = j(m + n) p (m, n)
(b) Establish the following orthogonal property of Hermite polynomial: (03)
Y H{x)Hm(x)dx = 2nn\8m
4. (a) Show that the coefficient of tn in the expansion of the function (1 - 2xt + t2) Vl is the (03) Legendre Polynomial Pn(x) of degree n for | x | <1.
' (b) (03) Show that the function <f>n (x) = e 2 Ln (x)\ n = 0,1,2,.........form an orthonormal set of
functions in the interval 0 < x < oo i.e.
o
OR
2009-2010
B.Sc. (HONS.) (PART-III) EXAMINATION (PHYSICS)
MATHEMATICAL METHODS (PH-307)
Maximum Marks : 40 Duration : Three Hours
NOTE: (i) Answer ALL questions.
(ii) Marks are indicated against each part.
1. (a) State and prove Cauchys integral theorem. > (04)
(b) Assuming that f(z) is analytic on and within a closed contour c and that point z<> is (03) within c, show that:
rf\z)dz r f\z)dz ; z-*o hz~zo)2
l. (a) Define an analytic function and obtain the Cauchy-Riemann differential equations. (04)
(b) Using Taylor expansion show that: (Pty
1 CO
i-t h
2. (a) State and prove Stokes theorem of vector analysis. Show that Greens theorem in the (04)
plane is the special case of Stokes theorem.
(b) Show that gradient of a differentiable scalar function f at a point P of surface S. (03) f(x,y,z)=constant, is a normal vector of S at P.
3. (a) Define Beta and Gamma functions and show that: (03)
|(n) {(in) - |("m + n) (3 (m, n)
(b) Establish the following orthogonal property of Hermite polynomial: (03)
aj
\exlH(x)Hm(x)dx = 42nn\Sm
4. (a) Show that the coefficient of tn in the expansion of the function (1 - 2xt + t2) /j is the (03) Legendre Polynomial Pn(x) of degree n for | x | < 1.
' (b) zl (03) Show that the function <j>n (x) = e 2 Ln (x); n = 0,1,2,.........form an orthonormal set of
oo
functions in the interval 0 < x < oo i.e.
OR
4. (a) Obtain a solution of Bessels equation :
x2y'! + xy/ + (x2 - n2) y = 0
(03
(03
(04
by series substitution method.
(b) Find the Rodrigues formula for Legendre Polynomials.
5. (a) Find the Fourier coefficients of the periodic function :
and f(x+27i) = f(x)
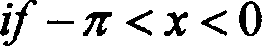
k if 0 < x < n
Hence prove that = 1---1----
4 3 5 7
(b) The vibration of an elastic string are governed by the one dimensional wave equation (03
r- = c 7
dt2 dx2
Where u(x, t) is the displacement of string. Find the displacement u(x, t) for boundary
condition u(0, t) = u(L, t)=0 and u(x,0)=f(x) and [(=0 = g(x).
dt
OR
(b) Solve Laplaces equation Vzv = 0 where v represents he temperature at point (x, y) on a (03 thin metal plate that is bounded by the lines x = 0, x = S, y = 0 and y = h subject to the boundary conditions v = 0 at x = 0 and x = S, v = 0aty = 0, v = F(x) at y = h.
6. (a) A linear oscillator equation y" + to2y = 0 with the boundary conditions y(0) = 0 and (04 y(b)=0 is represented by an integral equation :
b
y(x) = co2 \k{x,t)y{t)dt
o
Find the kernel k (x, t).
OR
(a) Give the general procedure for solving Fredholms equations of the second kind with (O' separable kernels.
(b) Solve the equation :
<t>(x) = x + Vi J(/ + x)<f>{t)dl
-i
I
|
Attachment: |
| Earning: Approval pending. |
