Indian School of Mines 2004 B.Tech Computer Science and Engineering IV CSE and IV M.ScM&C(Winter semester) - Question Paper
Examination:IV B.Tech. CSE and IV M.Sc. M&C(Winter semester)
Session:2003-04
Subject: Algorithm Design and Analysis
Time:3 Hours
Max. Marks: 100
-----------------------------
Max. Marks: 100
Session: 2003 - 2004
Examination: IV B. Tech (CSE) and IV M. Sc (M&C) Subject: Algorithm1Design and Analysis Timc/hSurs
Group - A (Answer all questions)
1. J)j)Derive the time complexity of a recursive algorithm for summing n numbers by
.step coun! method.
fy) Give a proof tliat shows the rucurrcncc relation T(n)~ mT(n/2) + an' is satisfied by T(n) = 0(noy7K).
>c) What is the smallest value of n such that an algorillmi whose running time is JOOri runs faster than an algorithm whose running time is T on the same machine? (4+5+3)
2. Jp) Write the working principle of tlie greedy method. How does it differ from the
dynamic programming method?
b) Hxplain the notion of the tree vertex problem. Write a greedy algorithm for this* problem and illustrate it with suitable example. (4-8)
3. (<0 Define the general Knapsack problem and write the different applications of
it? Write a greedy algorithm for this problem and derive its time complexity.
(b) Trace your algorithm in part (a) lo find an optimal solution for n ~ 7, m 15, iPhPz ...,/>= (10, 5. 15, 7, 6, 1X: 3)and(w/. w* .... wn=(2, 3, 5. 1, 1: 4. 1) where p and w are tlie profit and weight vectors respectively. (5*7)
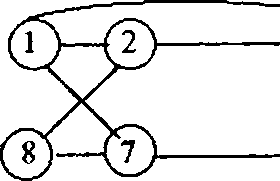
4. (a) Present a backtrack algorithm to find all Hamiltonian cyclcs of a connected ' graph with n vortices. What is its woisl-ea.se time complexity?
Jp) Draw the portion of the state space tree generated by your algorithm in part (a) for the following graph? (517)
5. Write some applications of a convex hull. Explain the extreme point method to find tlie convex hull of a sej jtaints in a plane.
'tk/ Present a divide and concjucr aJuorithrr? f***!" findins convex hull ip a plane, derive its time complexity and compare it with the extreme point method. (5-7)
Continued...
GroupB (Answer any two questions)
6. awBxplain why Dijkstras algorithm for single source shortest paths may not be always applicable to solve all pairs shortest paths problem.
Present the dynamic programming formulation for all pairs shortest paths problem. Write the coiTesponding algorithm and derive its time complexity.
(c) Trace your algorithm in part (h) for the following graph

(3+1 )+7)
7, (a) What are the advantages and disadvantages of the backtrack method? Wiich
'-y type oi the problems is this method suitable? Write a control abstracts n a backtrack algorithm.
(J# YYliat do you mean by AT-compklc problems? llovv does it different fr un A-Hard problems? Give some examples of A'P-complete problems. Writi a non-deterministic algorithm for the Knapsack problem and derive its tii ic complexity. (10+1 >)
8. a) Present tlie dynamic programming formulation for Traveling Salesperso i
Problem (TSP) and vvrile the corresponding algorithm. What is the tim complexity of the algorithm?
Given the following initial and final arrangements describe the LC-search solution of the 15-puzzel problem. Show the portion of the state space tree generated during this search. (10+10)
| ||||||||||||||||
|
Final |
| ||||||||||||||||
|
Initial |
Mailer Daemon 2008 |
|
Attachment: |
| Earning: Approval pending. |
