Indian School of Mines 2008 B.Tech Mining Engineering 3rd__Mining_07-08 - Question Paper
14
6
5
10
5
14
6
The stresses on the element [ in fig. 3 ] are ax = 3 MPa , ay i 1 MPa, T*y = 2 MPa. Find the stresses on a plane formed a; 22.5 with left vertical axis
through the element, (use formula approach ).
For the same element find the principal stresses and their directions (use Mohr's circle approach).
Establish the relationshipbetween the Young Modulus, E and shear modulus, G.
A 45 strain gauge rosette records the strains as 0 ~ 350 jj., 645 2l3y. , 690 = 250 n, n = lO*6 . Determine the 2-D strain state at that point. Also find the
principal strains at that point ---------]
%
|
12 12 |
 |
principal strains at that pomi__
Compare the maximum shear stress in a thin circuiar tube of mean radius
with constant wall thickness t when Tm*x is calculated by approximate thin
tube thcor> [of Bredt tb] and Tmitt is calculated from commonly used
torsion theory [of Colomb =* Tc]- If P find rhe values of tb /tc for
P * 5,10 and 20. Note, r t.
A cantilever beam of length. L and constant strength is required to carry a concentrated load, p, ai its free end. It is having a varying rectangular cross-section (Fig. 4J. Derive the expression for its theoretical shape neglecting the
shear stresses.
A simply supported beam has 5m span and a uniform T-section [Fig. 5] of 100 mm width and 150 mm depth with flange thickness, if " 25 mm, and 1 web thickness. tw 12 mm. If the limiting bending stresses for the beam I material are taken as 80 MPa in compression and 160 MPa in tension, find
the maximum u.d.l. this beam can safely carry.
A steei bar of rectangular cross-section 40 mm x 50 mm has pinpin end condition. It is used to carry axiaJ compressive load. If the proporfional limit for the material is 230 MPa and * 210 OPa, determine the minimum length for which Euler's equation can be applied to evaluate the buckling
, load. If the evaluated length is increased to twice the value whai will he ihe.
J
,r latest rnfo about
Ill B. TECH | MECH/ MM/ PET/ MIN/ MLE/ELECT/ENV] ExSSSoTON Subject MECHANICS OF SOLIDS | MMC 131011 Max. M ,
Max, Time : 3 Hours Instructions : Answer any TWO questions from GROUP -A, and ALL from GROUP B
Assume missing data ( if any ) suitably. All parts of a question MUST be completed In a sequence of the question and in continuation, for full marks. Marks will be deducted otherwlte.
%s~ ~V Questions for GROUP - A I ANSWER ANY TWO |
A rigid prismatic bar of length 3b I Fig. \] is held to horizontal position by two tic rods: (1) ~A1 rod and (2)- Mg rod of length Li and Lj respectively.
Their respective diameters arc d( and d2 and Youngs modulii arc E\ and E2.
Find the expression for maximum allowable load, Pm , at the free end, B ( without causing yielding of the rods ). [Preferably use flexibility method ].
Find the value of Pmax, if Li * 0.4m, L2 0.3m. di * 4.0mm, d2 3.0mm,
Ej = 72 GPa. Ei - 45 GPa, <*\ | M<>vt = 200 MPa.
\ 3. (a) 1 Evaluate and draw the S.F.D. and B.M.D. for the beam shown in [ Fig. 2.a ] and locate the point of contruflexure.
( b ) j Find the maximum deflection for a cantilever beam [Fig. 2 (b)] whose 1n.a. * 46.2 x 1 O6 m4 and E = 12 GPa ' (use foniula superposition method, preferably).
Schematically draw Lames lines ( i ) to represent a solution to a general thick cylinder problem, (ii ) to represent the solution when the thick cylinder is under internal and external pressure.
State the assumptions associated with the determination of stresses in a thick cylinder problem.
Derive the Lames equations for a thick cylinder analysis.
Questions for GROUP - B f ANSWER ALL THE QUESTIONS 1
' 4. (a)
00
I I %
I
5. (a) (b)
6. (a)
<b)
*
H
Al-md
<jU/ rod
/
/
/
/
/
/
N
l)i *
) ! *
It
t
Mu. I.
25 kN/m
m
r-f-r-ri m * * i ~i
6 m
(Qrnemiwn jwprr
SRMK8T
Gttmmtftoai 4 Scmeata
Subject (Block kftton)_
Innmctiom, if my An
an
Section (if y)_
l:ig. 2(a)
|The cranK
and the c 30 0 RPM 1 ha 3 turn' accaler a<
a) Veloc
b) angul conn o
c) acoil
Finrt an shoe W
I'h*? 'fart ricte*
3 6
and bic
Coef fi<
COm39
CYlc Draw, i
followc front Ut
4 kiN +
3 kN/m
< rt I'ft t"t I1TITT
C
4.
A
h-
800 mm
400 mm
Fig. 2(b)
|
Ox-4 | 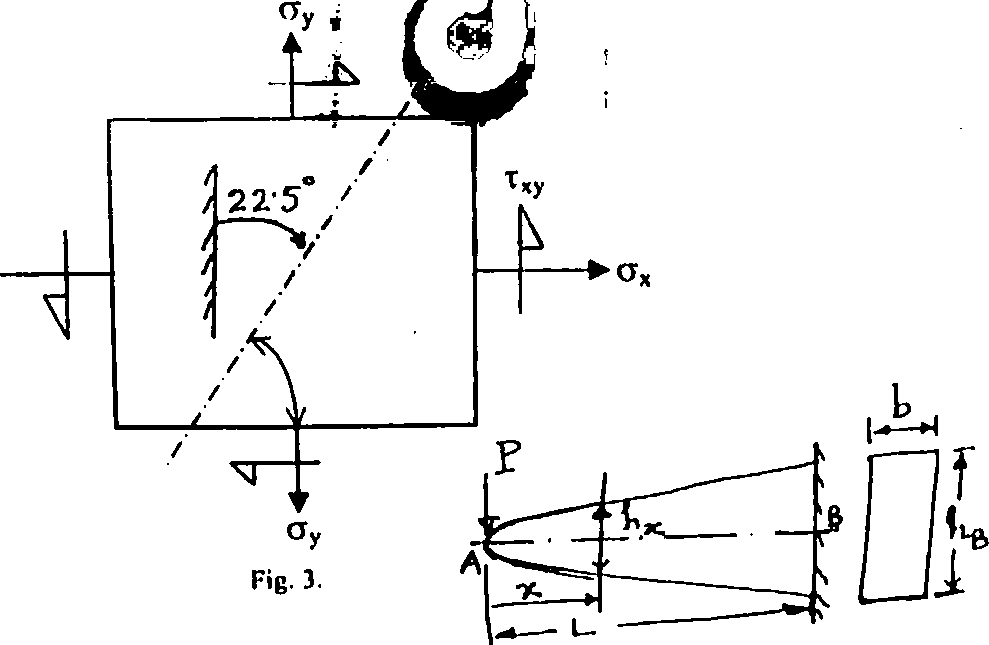 |
2
|
100 | |
 |
25 * C f N.A X lint* (Kef) |
|
All dimension* arc In mm. | |
rig >
SEMESTER: MONSOON SirSKHiN
Examination & Semester: 111 Sin,. B. Tech. (Common) Tim*. l||nUri 'H Subject: MATHEMATICS- .I. M mSI"*,
Instructions: (i) Use separate Answer Nook lor each section.
(ii) Figures in the margin indicate full marks.
Section-A
(Analysis of Complex ViirinMc: murks)
Question No. I is compulsory. Attempt any Two from the rest.
Ql (i) Show that the polar form of Cauchv-Riemann equations
rH# I dv cH* I du
are
rd 0 (5)
/(z-l)(z-2)3 ,c:l2_2| = l/2 (4)
(iii) Find the bilinear transformation which maps 1, i, - I to 2, i, -2 respectively. Also find the fixed point of the transformation.
dr r d9 ' dr zdz
(ii) Evaluate J
.(5)
(iv) Find the Laurents expansion of f(z) =- in the region l<|z+l|<3
(z + l)z(z -2)
(5)
, %cosxdx _
02. Evaluate =-r-, using Contour integration. (7)
>x2+a2
i
Q3. Evaluate f/ - , where C is liie circle lz| = 4.
2(z2+x2Y
(7)
Q4. If f (z) = u + i v is an analytic function of z = x +i y and f any function of x and y with differentiable coefficient of first and second order derivatives then proven that t2 /. \2 f/ ,
\f(4 (7)
|
dy/' |
k> II |
2 | |
|
I tyj |
v du ) V dv J |
dy/
dx
Section B (33 Marks)
(Special functions)
Q. Nos. . to 4 are compulsory. Attempt any TWO from the rest.
I.M
dx * terms of an elliptic integral ' Vcosx
Express / = I
n v
2. Prove that
in
(.n
j J,{x\dx = r).C is a constant of integration.
(5)
f.M
(7)
O)
t.M
3. Prove thai
V/ u . 2(w + l)
-i
4. Prove that
2n J(x) X|J-|(X) * Jn.|(X>|. ,
5. Using I robenius method solve the equation
xy" + y' *- xy " 0.
6. Show that
I > - -t xsin0t)<ty.n being an integer.
0) Expand !Tx) 0.
In terms of Legendre polynomial* upto the degree 3.
l,Pr0VCthat w 1.3.5.....I)
M) 2.4.6......(2m)
(Laplace Transform and P.D.E: 34 MARKS) Question Nos. 1 to 3 are compulsory. Attempt any Two from the rest.
 |
Questions |
|
Let F(t) | |
= - where F(t) is periodic function with
6,2 < t < 4
period T = 4. Find the |aplace transform of F(t).
1
2.
(*-l)3fr + 2)
Find the inverse feiplace transform of
Using Laplace transform technique solve
3.
fr+2r+/r = o, r(0) = i, y(tt) = o
Using Laplace transform technique solve
4.
= 3, Ux(0,t) = 0,U(|,/) = 0
if U(x,0) = 20 cos 3x-5 cos 9x
A square plate is bounded by the lines x=0, y=0, x=20 and y = 20. Its faces are insulated. The temperature along the upper horizontal edge is given by u(x,20) = x(20 x) when 0 < x < 20, while the other
edges are kept at 0 C. Using variable separable method find the steady state temperature at any point on the plate.
A tightly stretched string with fixed end points x=0and x=l is initially at rest into its equilibrium position. If it is vibrating by giving to each
anv P'nts 3 v*oc>ty x(l-x), find the displacement of the string at
variables06 X rm ne Cn an **me * method of separation of
w

SEMESTER: MONSOON* iTQcirwi *AA Page No 1/3
Examination & Semester: B.Tech.JJIlKlrcirical K,. 2007-2008
Mining. M,-.,
Tim: 3 Hours Subject: APPLIED .................. ......
1. Attempt any TWO questions from Group A (O 1 -3 anH ai i .
2. Assume missing data, suitably, if any. - s 10ns from Group B (Q.4-8).
:. Assume missing data, suitably, if any.
3. Notations have their usual meanings, unless stated otherwise.
4. Use of Steam Table is permitted.
GROUP - A (Answer any two questions)
3. Notations have their usual meanines. nnlpcc
1.
It is well established that the adiabatic and reversible volume change of an ideal gas {R,c )
in a cylinder and piston apparatus follows the path PVr = constant, where y = ~. Real
<\
processes, however, depart from this path; the actual path is named polytropic and is
represented by the function PV" = constant, where n is a constant (n * y). The mass ofthe
ideal gas is m, the mass of the cylinder wall is M, and the specific heat of the wall material is c. At any instant during the expansion or compression process, the ideal gas and the wall material are in mutual thermal equilibrium. Furthermore, the combined system (ideal gfcs and the wall material) does not exchange heat with its surroundings. The
expansion or compression process is sufficiently slow so that jSW| = \PdV\ is practically valid.
(a) Show that the path of the polytropic process is designated by n -1 + + Mc,mc
(b) How large or small should the wall heat capacity be if the path is to approach
| PVT = constant? . ,
;<C) Evaluate the entropy change dS for the combined system dg the
change in volume from V to (V + dV) *
- tn Hecide whether the process executed by
(d) Invoke the Second Law of Thermodynam
the combined system is reversible or irreversij--__--= constant to a
Steam at a pressure of 15 bar and 250 C expands pjane and find the
pressure 1.5 bar. Sketch the process path in entropy change. The mass of the conditions, (b) w6rk done, (c) heat transfer and, (d) entr py
is 0.9 kg. ___________f30 bar and
3. 1 In a Rankine cycle, the steam at miet~to
exhaust pressure is 0.24 bar. Sketch e p efficiency, and (d) e
(a) the pump work, (b) turbine power, (c) R**' flow? Assume a flow rate of 10 kg/s.
GROUP B (Answer all questions)
(a) According to Newtons Second Law of Motion, the resultant of all forces isTp' the time rate of change in the momentum of the system. Projecting this statement in 0n
direction of interest *, we have - 2>P, + (W, ). In similar,',,
in out Of uy
with this equation cast the First Law of Thermodynamics as an energy conserve equation for an open system. Therefrom write down an expression for the First La Thermodynamics reduced for a closed system. W
(b) The work and heat exchange involved by a system in a process A are 20 kj and kJ respectively. Another process B between the same final conditions involves ah input of 9 kJ. Determine the change in internal energy involved and also the work H during the process B Prove that if a cycle is formed employing process A and B T First Law of Thermodynamics is obeyed e
I
i 11 31 LU IT VI * ~ ~ ---J ~
(a) Define COP of a heat pump and refrigerator. Hence argue that COP of a heat pump is always greater than that of a refrigerator.
5.
(b) In a cascaded system, cycles are coupled in series such that the heat rejected by the topping cycles are employed by the bottoming cycles. Assuming the efficiency of the ilh cycle to be tj, arrive at an expression for the overall efficiency rj of the combined cycle
n
consisting of n cycles as 77 = 1 -m-o.) . Taking a numerical example for two cycles with 7, = 0.25 and t}2 = 0.30 show that there remains a true gain in overall efficiency.
(a) A closed system type gas turbine er plant operii~on BTayton cycle Derive an expression for thermal efficiency involving pressure ratio as a
6.
that the optimum pressure ratio for maximum u,a * *
permissible pressure ratio. 1S s<3uare root of maximum
(b) Considering air to be the working fluid with r tr- a a
temnmtnrpc m . U , p/cv -l-4> and normally encountered
temperatures in gas turbine to be 288 K and 1 non v 1 . / .
thermal efficiency and net work out it, to scale) the variation of
tworkoutput Wlthrespect tQ the var.at.on Qfp;essure e
> 1(a) Sketch various'ihrSr?7r~-7r_________
I md Dual cycle. From the effkLr seParateiy Tottocycle, Dkxl
efficiency expressions for Otto and Dif S eXpreSSion of Dual cycle deduce the
(b) An air standard dual cycle h COrolIaries-
all other cardmal.points ofT Volume- Estimate lransferred to air at constant of the cycle. Assume c n Cyle' Thus calculate the f Ut?s and temperatures at
wfe1* i.noSS1 fracUo" kNW in a boiler rxded
Tly calorific valueTf cl?? '* '98' Th= f
*-=Pori ,s 3I0 U/kg. Determined*
1
I
Mailerdaemon I ForJZT7~-----
'ND'ArlS<iH001' " MIN,!S ,,N|VKRSrrv
Department of Mining lingineerinjj
Examination: HI Semester B.Tech (MB) (Combined coutal
Semester: Monsoon Semester Session* 20074)8
Subject Exploration Drilling and Rock Brc.kjnc (Mrr Time 3 Hours
im. ijiui) Marks 100
Q Question . _ ,
Scction- A Mafks
Attempt any two questions 1 Explain the importance of geology in open cast blast design Design a blast for coal measure rock strata having 14m bench height, average compressive strength 80 MPa, hole diameter 165 mm. (assume other (20) parameters - like type of excavator etc.)
2. (a) What do you understand by wire line drilling? State its merits over (10) other methods of core drilling
(b) With the help of a sketch explain the hydraulic feed mechanism (10) used in diamond core drilling.
3 Briefly discuss the rock properties that affect drilling. What do you understand by disability of rocks? Discuss various parameters to be (20)
considered while selecting a dnll rig.
Section - B
All questions are compulsory
4 What do you understand by bfusldm Degree fll (10) different from other explosives? Why PI canno!
gassy coal mines?
r used in dnlling with their (10)
5 Discuss the different types of aug
suitability.
A in Botd and v'orkm&S0)
6 Discuss the blasting techniques used
COalmineS c9 Fxnlain w.lh the (10)
Und..d "-? EW
7.
help of sketches a delay detonator.
Compare between the [ollowl'i jves (5)
(a) Emulsion and NG-based xp han)rner drilling (5)
(b, Down the hole dnllmg and Top (J)
(c) Diagonal and v-pattem o
(d) Button bit and tn-cone rock roll
Examination: III B.Tech Mining Engineering
Session: 2007-____ Monsoon Semasto'
Time: 3 hrs
Subject: Geology I (Physical Geology and StructuiGij----art<8:1Q0
Answer any two questions from Part -1 and all questions from Part-11
----VAVCT-X
Marks
|
1 |
Define different elements of a fold. Describe the geometrical classification of folds. |
~20] |
|
2 |
What are the tectonic divisions of India? Describe the characteristic features of peninsular India. |
20 |
|
3 |
What is Nebular theory? Give a brief account about interior of the earth |
20 | |
|
PART- II I | ||
How joints are different from faults? Describe the classification of joints in relation to deformation
15
15
Give a brief account on geological works of rivers.
Write short notes on any three of the following
(3X5)=15
(a) Plate boundaries.
(b) Physical and chemical weathering
(c) Double star hypothesis
(d ) Nonconformity and disconformity
(3X5)=15
Attempt any three of the following:
(a) What is rock Cleavage?
(b) What is Barchan?
(d) Determine the stnke and dip of an oil bearing strata on the basis of
exploratory drilling data pairs.
The apparent dip values are as follows.
Direction of Apparent dip
N80 K N60 W
36 degree
9 * -\r- *
Mailerdaemon | For latest info about the college visit www.mailerdaemo
|
Attachment: |
| Earning: Approval pending. |
