Indian Institute of Technology Kharagpur (IIT-K) 2008 B.Tech Mechanical Engineering Mechanics Part -1 - Question Paper
Mechanics
first year
Mechanical Engineering Department
Indian Institute of Technology ,Kharagpur
Both part of the paper is attached beneath.
V INDIAN INSTITUTE OF TECHNOLOGY, Kharagpur
Date: / /2008FN/AN End Semester (Spring) 2008 Time: 3 hrs Full Marks: 100 Dept.: 1st yr B.tech. / B.arch /Int. M. Sc./DD Subject Name: Mechanics Subject No.: ME10001
All questions carry equal marks (25 X 4). Marks distribution for each question is indicated within brackets. Asstune any suitable data that may be required for solution, stating clear justifications.
Question paper has 2 pages. Answer all questions.
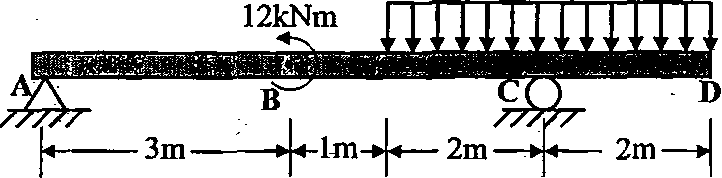
1(a). Draw the shear force and bending moment diagram for the beam subjected to loading conditions as shown in Figure 1 a. (18)
|
lkN/m |
 |
|
Figure la |
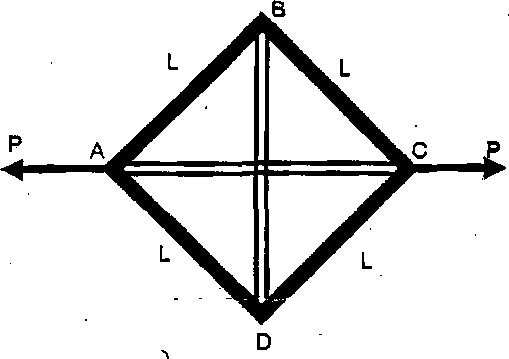
1(b). A Wheatstone bridge like square is formed of rigid rods each of length L and connected by pin joints (Fig. lb). Two identical elastic rods with area of cross section A and modulus of elasticity E form the diagonals. A tensile force P is applied to the structure as shown. The compression observed in the diagonal BD is Abd. Find the force P. You may consider change in lengths to be small as compared to the original lengths in order to simplify the answer using binomial theorem. (7)
 |
|
Figure lb |
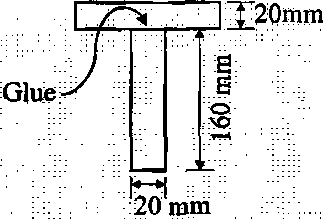
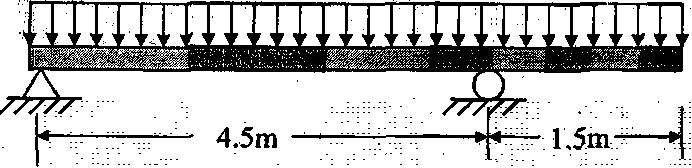
2(a). The simply supported overhang beam shown in Figure 2a is made from two slabs of the same isotropic material with rectangular cross-section glued together to form a T-section. The geometrical dimensions of the section are shown in the picture to the right.
|
IkN/m | ||||
 | ||||
|
Figure 2a (a) Determine the necessary section properties (b) Draw the bending moment and shear force diagrams (c) Find the maximum tensile stress in the beam and locate the corresponding position along the beam axis. (d) Find the maximum compressive stress in the beam and locate the corresponding position along the beam axis. (e) Find the maximum shear stress in the interface (glued joint) of the T-section and locate the corresponding position along the beam axis. . contd p/2
You are here:
PAPER
 Indian Institute of Technology Kharagpur (IIT-K) 2008 B.Tech Mechanical Engineering Mechanics Part -1 - Question Paper
|