Indian Institute of Technology Guwahati (IIT-G) 2006 JAM Physics - Question Paper
JAM 2006 Physics
Full ques. Paper in attachment
PHYSICS TEST PAPER
Useful Data
1. Speed of light in free space, c = 3 x 108 m s-1
2. Plancks constant, h = 6.6 x 10"34 J s
3. Electron charge, e = 1.6 x 10-19 C
4. Electron mass, me = 9.1 x 10-31 kg
5. Use e3 - 20
NOTE: Attempt ALL the 25 questions. Questi ons 1-15 (objective questions) carry six marks each and questions 16-25 (subjective questions) carry twenty one marks each.
Write the answers to the objective questions in the Answer Table for Objective Questions provided on page 12 only.
1. In a crystalline solid, the energy band structure (E-k relation) for an electron of mass m
h2k(2k - 3)
is given by E =-. The effective mass of the electron in the crystal is
2m
(A) m 2
(B) m
3
m
(C) i
(D) 2 m
2. Two electric dipoles P1 and P2 are placed at (0, 0, 0) and (1, 0, 0) respectively, with both of them pointing in the +z direction. Without changing the orientations of the dipoles, P2 is moved to (0, 2, 0). The ratio of the electrostatic potential energy of the dipoles after moving to that before moving is
(A)
(B)
(C)
(D)
16
1
2
1
4
1
8
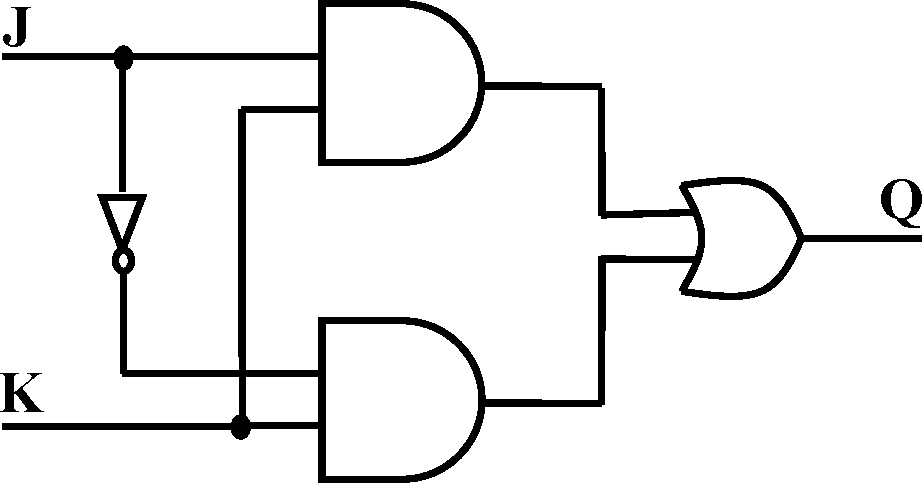
|
J |
K |
Q |
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
|
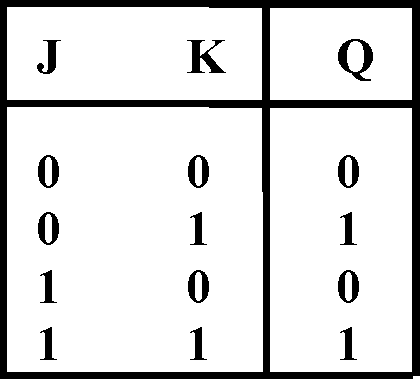
J |
K |
Q |
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
(B)
At a given point in space the total light wave is composed of three phasors P1 = a,
a a _ . q
e 1 . The intensity of light at this point is
P2 = e1 and P3 =
2 2 3 2
|
(A) |
4 a2 cos2 |
|
(B) |
4 a2 cos4 | |
|
(C) |
a2 cos2 (q) |
|
(D) |
4 a2 cos2 (2 |
A small magnetic dipole is kept at the origin in the x-y plane. One wire Li is located at z = _ a in the x-z plane with a current I flowing in the positive x direction. Another wire L2 is at z = + a in y-z plane with the same current I as in Lis flowing in the positive y direction. The angle <p made by the magnetic dipole with respect to the positive x-axis is
(A) 225
(B) 120
(C) 45
(D) 270
The ratio of the inner radii of two glass tubes of same length is V2. A fluid of viscosity 8.0cP flows through the first tube, and another fluid of viscosity 0.8cP flows through the second one when equal pressure difference is applied across both of them. The ratio of the flow rate in the first tube to that in the second tube is
|
(A) |
1.6 |
|
(B) |
10 V2 |
|
(C) |
V2 |
|
(D) |
0.4 |
The relation between angular frequency o and wave number k for given type of waves is (o2 =ak + P k3. The wave number k0 for which the phase velocity equals the group velocity is
|
a | ||||||||||
| ||||||||||
(A)
(C)
(D)
A neutron of mass mn = 10 kg is moving inside a nucleus. Assume the nucleus to be a
a
10-
34
Js and
cubical box of size 10 14 m with impenetrable walls. Take h 1MeV 10-13 J. An estimate of the energy in MeV of the neutron is
(A)
(B)
(C)
(D)
80 MeV
MeV
8
8 MeV
MeV 80
A spring-mass system has undamped natural angular frequency o)0 = 100 rad s-1. The solution x(t) at critical damping is given by x(t) = x0(1 + a>0 t) exp(-01), where x0 is a constant. The system experiences the maximum damping force at time
9.
0.01 s 0.1 s
0.01 s 0.1 n s
(A)
(B)
(C)
(D)
In an intrinsic semiconductor, the free carrier concentration n (in cm- ) varies with temperature T (in Kelvin) as shown in the figure below. The band gap of the
10.
semiconductor is (use Boltzmann constant kB = 8.625 x 10 5 eV K-1)
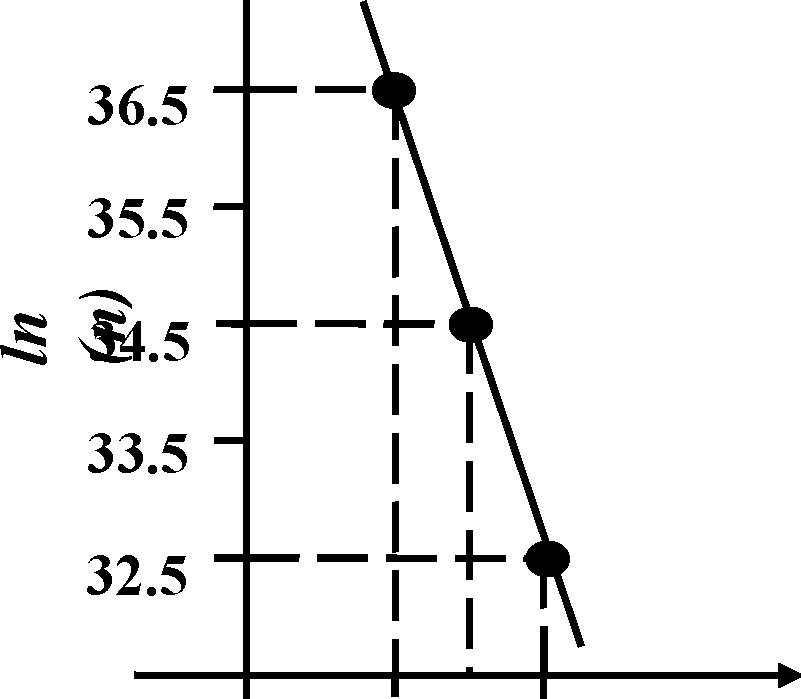
|
(A) |
1.44 |
eV |
|
(B) |
0.72 |
eV |
|
(C) |
1.38 |
eV |
|
(D) |
0.69 |
eV |
11. E(x, y, z, t) = A(3 i+ 4 j)exp\i(t - kz)] represents an electromagnetic wave. Possible directions of the fast axis of a quarter wave plate which converts this wave into a circularly polarized wave are
(A) 72[ [ +j ] and 72[-1 +7 j]
(B) 72[3 [ +4 j] and 72[41 - 3 j]
(C) 72[3 [ - 4 j ] and 72[41 +3 j ]
(D) 72[7 [ - j] and 72[ i + 7j]
12. A particle of rest mass m0 is moving uniformly in a straight line with relativistic velocity (c, where c is the velocity of light in vacuum and 0 < // < 1. The phase velocity of the de Broglie wave associated with the particle is
|
(A) |
/c c |
|
(B) |
( |
|
(C) |
c |
|
(D) |
c |
13. Electrons of energy E coming in from x = - ro impinge upon a potential barrier of width 2a and height V0 centered at the origin with V0 >E, as shown in the figure below. Let
Jim (V0 - E ) . k = -. In the region - a < x < a, the wave function for the electrons is a
h
linear combination of
k
V0
x
a
(A) ekx and e
(B) elkx and e
- kx
kx
(C) elkx and e- lkx
(D) e-lkx and ekx
A solid melts into a liquid via first order phase transition. The relationship between the pressure P and the temperature T of the phase transition isP = -2T + P0, where P0 is a constant. The entropy change associated with the phase transition is 1.0 J mole-1 K-1. The
Clausius-Clapeyron equation for the latent heat is L = T| dP I Av. Here Av = vliquid - vsolid
V dT J
is the change in molar volume at the phase transition. The correct statement relating the values of the volumes is
(A) vliquid = vsolid
(B) vliquid = vsolid 1
(C) vliquid = vsolid--
2
(D) vliquid = vsolid + 2
The symmetric part of P = I (a 2 b) is
15.
C a2 2 ba 1 Kba 1 b2 2 j a(a 2) b
(A)
(B)
(C)
(D)
2
b
b
2
Vb(a 1) J
C a(a 2) b(a 1) b(a 1) b2
b
J
16. Consider a Body Centered Cubic (BCC) crystal with lattice constant a. Determine
(a) the Miller indices for the (1, 0, 0) plane,
[9]
[12]
(b) the number of atoms per unit area in the (1, 1, 1) plane.
= nRT, while during an adiabatic process
17. The equation of state of a gas is P
the gas obeysP VY = K, where a and K are positive constants. All other symbols have their usual meaning. Find the work done by the gas when it is expanded first isothermally
P
from (P, V) to (Pi, 2V) and then adiabatically from (Pi, 2V) to (-, Vj), where P1 < P.
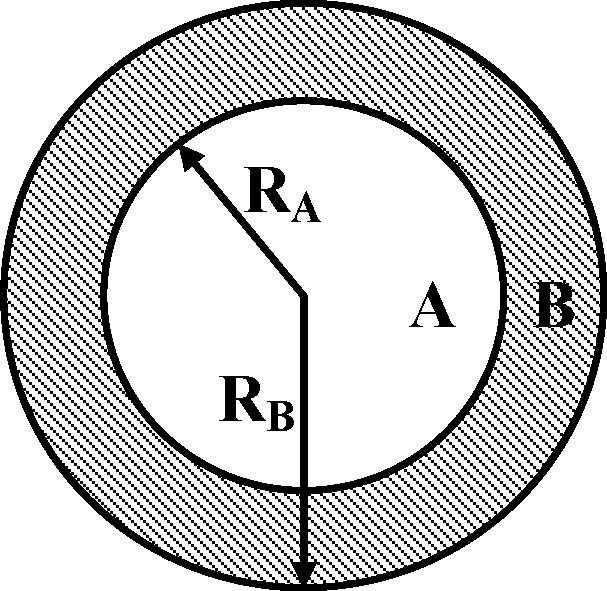
18. A conducting sphere of radius RA has a charge Q. It is surrounded by a dielectric spherical shell of inner radius RA and outer radius RB (as shown in the figure below) having electrical permittivity s(r) = s0 r .
|
(a) Find the surface bound charge density at r = RA. [12] (b) Find the total electrostatic energy stored in the dielectric (region B). [9] |
 |
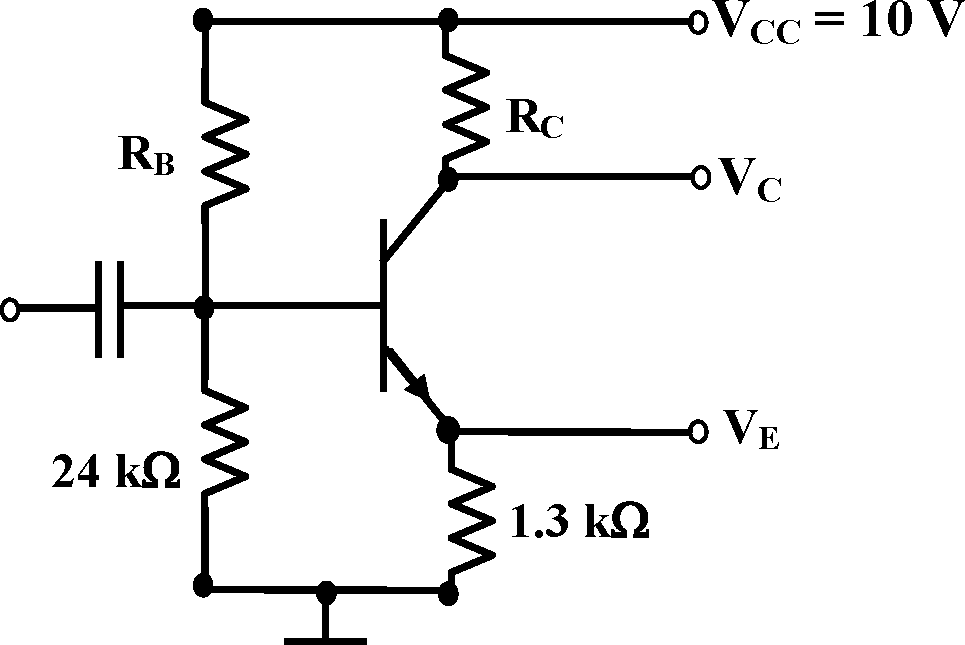
19. For the transistor circuit shown below, evaluate VE, RB and Rc, given IC =1 mA, Vce = 3.8 V, VBE = 0.7 V and Vcc = 10 V. Use the approximation Ic ~ IE
[21]
20. For the vector field V = xz2 i - yz2j + z (x2 -y2 )k ,
(a) calculate the volume integral of the divergence of V over the region defined by
- a < x < a, - b < y < b and 0 < z < c .
r [12]
(b) calculate the flux of V out of the region through the surface at z = c. Hence deduce the net flux through the rest of the boundary of the region. [9]
21. The spherical surface of a plano-convex lens of radius of curvature R = 1m is gently placed on a flat plate. The space between them is filled with a transparent liquid of refractive index 1.55. The refractive indices of the lens and the flat plate are 1.5 and 1.6 respectively. The radius of the sixteenth dark Newtons ring in the reflected light of wavelength X is found to be V5mm.
(a) Determine the wavelength X (in microns) of the light. [12]
(b) Now the transparent liquid is completely removed from the space between the lens and the flat plate. Find the radius (in mm) of the twentieth dark ring in the reflected light after this change. [9]
22. A resistor of 1 kQ and an inductor of 5 mH are connected in series with a battery of emf 4 V through a switch. The switch is closed at time t = 0. In the following, you may use e3 - 20.
(a) Find the current flowing in the circuit at t = 15 micro-second. [9]
(b) Find the heat dissipated through the resistor during the first 15 micro-second.
[12]
23. A photon of energy Eph collides with an electron at rest and gets scattered at an angle 60 with respect to the direction of the incident photon. The ratio of the relativistic kinetic energy T of the recoiled electron and the incident photon energy Eph is 0.05.
(a) Determine the wavelength of the incident photon in terms of the Compton
r h }
wavelength Xc =- , where h, me, c are Plancks constant, electron rest mass
I meC)
and velocity of light respectively. [12]
(b) What is the total energy Ee of the recoiled electron in units of its rest mass ?
[9]
- 3
24. A particle moves in a plane with velocity v = vrr + v00 such that vr = -4v0. The time
dependence of the magnitude of the velocity | v | = 5t. It is given that r = 1, 0 = 0 and vr > 0 at t = 0. (In the following, you may use e3 - 20.)
(a) Determine the traj ectory r(0) of the particle. [9]
(b) At what time will 0 become 4 radian? [12]
25. A body of mass 1 kg moves under the influence of a central force, with a potential energy
function V(r) = - exp( 3r /2) Joule, where r is in meters. It is found to move in a
5r
circular orbit of radius r = 2 m. (In the following, you may use e3 - 20).
(a) Find its angular momentum L and total energy E. [12]
(b) A piece of mass m1 = 0.5 kg breaks off suddenly from the body and begins to fall radially inwards with velocity v = 10 cm s-1. What are the values of angular momentum L2 and total energy E2 of the remaining piece, assuming that the potential energy function remains the same? [9]
9
|
Attachment: |
| Earning: Approval pending. |
