Indian Institute of Technology Guwahati (IIT-G) 2006 JAM Master in Computer Applications - Question Paper
JAM 2006 Master in Computer Applications
Full ques. Paper in attachment
MASTER IN COMPUTER APPLICATIONS TEST PAPER
(A) 2
(B) 14
(C) 28
(D) 29
d u
2. If u (t) = u1(t )i + u 2 (t) j + u3 (t)* is a unit vector and- 0, then the angle between u (t)
dt
. du . and-is
dt
(A) 0
3. The missing terms in the table
|
x |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
y(x) |
0 |
3 |
0 |
3 |
0 |
using a 4th degree interpolating polynomial are
(A) (-45, -192)
(B) (-45, - 576)
(C) (-90, -192)
(D) (-90, 576)
4. The differential equation
2ydx - (3y - 2x)dy = 0
is
(A) exact and homogeneous but not linear
(B) homogeneous and linear but not exact
(C) exact and linear but not homogeneous
(D) exact, homogeneous and linear
n
(A) f (x) has a local maxima at x =
6
n
(B) f (x) has a local minima at x =
5n
(C) f (x) has a local maxima at x =
3n
(D) f (x) has a local minima at x =
6. Let W be the subspace spanned by (2i, 0, 1, 2i), (0, 2i - 2, i - 3, 0), (-C4 over C. The dimension of W over C is
i, 1, 0, i)and (1, 1, 1, 1) in
(A) 1
(B) 2
(C) 3
(D) 4
7. If
2h
3 \ f (x) dx = h [a f (0) + b f (h) + c f (2h)]
0
for all polynomials f (x) of degree < 2, and h > 0, then (a,b, c) is
(A) (1, 2, 1)
(B) (1, 4, 1)
(C) (2, 2, 2)
(D) (2, 4, 1)
TO TO y
ne
-dydx is
0 x y
|
(A) |
0 |
|
(B) |
1 |
|
(C) |
2 |
|
(D) |
TO |
\
9. The function f (x,y) = x3 + 3xy2 - 4y3 - 15x has a local
(A) minima at (-V5, 0)
(B) minima at (V5, V5)
(C) maxima at (V5, 0)
(D) maxima at (-V5, 0)
10. The remainder obtained on dividing 21680 by 1763 is
(A) 1
(B) 3
(C) 13
(D) 31
11. The orthogonal trajectories of the curves y = 3x3 + x + c are
(A) 2 tan-1 3x + 3ln |y| = k
(B) 3tan-1 3x + 2ln |y| = k
(C) 3tan-1 3x - 2ln |y| = k
(D) 3ln |x| - 2 tan _13 y = k
12. The iterative formula to compute the reciprocal of a given positive real number a using Newton-Raphson method is
(A) x+1 = x (2 -ax)
(B) x+1 = xn (2 + ax )
(C) x+1 = x2 (2 -ax )
(D) x+1 = x2 (2 + ax )
13. If y1 (x) = 3yx) + 4y2(x) and y2 (x) = 4y1(x) + 3y2(x), then y1(x) is
(A) c1 ex + c2 e7x
(B) Cj ex + c2 e-x
(C) c1 e -x + c2 e7 x
(D) c1 e -x + c2 e x
14. Let G be a group of order 8 generated by a and b such that a4 = b2 = 1 and ba = a 3b. The order of the center of G is
(A) 1
(B) 2
(C) 4
(D) 8
15. The general solution of the differential equation
(x + y - 3)dx - (2x + 2y + 1)dy = 0
is
(A) ln |3x + 3 y - 2| + 3x + 6 y = k
(B) ln |3x + 3 y - 2| - 3x - 6 y = k
(C) 7ln |3x + 3 y - 2| + 3x + 6 y = k
(D) 7 ln |3x + 3 y - 2| - 3x + 6 y = k
16. The surface area of the solid generated by revolving the line segment y = x + 2 for 0 < x < 1 about the line y = 2 is
(A) V2 n
(B) 2n
(C) 2V2 n
(D) 4n
17. Let g(x) be the Maclaurins expansion of Sin2x. If Sin2x is approximated by g(x) so
that the error is at most 1250 x 10-4 for 0 < x <1, then the minimum number of non-zero
3 2
terms in g(x) is
(A) 2
(B) 3
(C) 4
(D) 5
18. Let f (x) = x2 +1, g (x) = x3 + x2 +1 and h( x) = x4 + x2 +1. Then
(A) f (x) and g (x) are reducible over 12
(B) g (x) and h( x) are reducible over 12
(C) f (x) and h( x) are reducible over 12
(D) f (x), g (x) and h( x) are reducible over 12
y"( x) - 4 y'( x) + 8 y( x) = 10 exCosx
is
(A) e2x (k1 Cos2x + k2 Sin2x) + ex (2 Cosx + Sinx)
(B) e2x (kj Cos2x + k2 Sin2x) + ex (2 Cosx - Sinx)
(C) e~2x (k1 Cos2x + k2 Sin2x) - ex (2 Cosx - Sinx)
(D) e -2 x (k1 Cos 2 x + k2 Sin2 x) + ex (2 Cosx + Sinx)
(1 2 3 4 5 6 7 8 9 10 11 12
. The cardinality of the orbit of 2
20. Let a = under a is
v2 10 8 5 9 3 6 11 4 12 1 7,
(A) 3
(B) 6
(C) 9
(D) 12
1 x 1
21. The value of the integral J --dx using Simpsons rule with h = 0.5 is
41
902
43
902
45
902
47
902
(A)
(B)
(C)
(D)
22. Let f (x, y) = lnjx + y and g (x, y) = x + y . Then the value of V 2(fg) at (1,0) is
(A) - 2
(B) 0
(C) 2
(D) 1
23. The general solution of the differential equation
(6x2 - e-y )dx + 2xye~y dy = 0
is
(A) x2 (2 x - e - y ) = c
(B) x2 (2 x + e - y2) = c
(C) x(2x2 + e- y2) = c
(D) x(2 x2 - e - y) = c
24. If
f (x, y) = \
x 3
--r, (x, y) * (0,0)
x + y
otherwise
0,
then at (0,0)
df cf
(A) and exist and are equal
dx dy
df df.
(B) and exist but not equal
dx dy
df df
(C) exists but does not
dx dy
df . df ,
(D) exists but does not
dy dx
25. Two teams A and B play a series of four matches. If the probability that team A wins
2
a match is 3, then the probability that team A wins three matches, loses one and the third win occurs in the fourth match is
(A) 27
27
(B) 27
27
(C)
81
32
(D)
81
26. The function
1
xaSin, x * 0 x
0, x = 0
f (x) =
is differentiable at x = 0 for all a in the interval
(A) (-<*>, 1]
(B) (-1, <*>)
(C) (1, <)
(D) [1, <*>)
27. A fair coin is tossed twice. Let A be the event that at least one tail appears and B be the event that both head and tail appear. Then P(A / B), the probability of A given B, is
1
(A) -
4
1
(B) -
(C)
(D)
2
2
3 1
|
28. The value of f (5) using Lagranges interpolation formula, given | ||||||||||
|
is
(A) - 3
(B) -1
( C) 1 <d) 2
29. Let F be a field. Given below are six statements about F.
1. F is a skew field
2. F is a group with respect to multiplication
3. F is an integral domain
4. F has zero divisors
5. F has no zero divisors
6. Only ideals of F are {0} and itself
In which of the following options all the statements are correct?
(A) 1, 2, 3
(B) 1, 3, 5
(C) 2, 4, 6
(D) 4, 5, 6
30. The work done by the force p = 3i - 2 j + 4k acting on a particle, if the particle is displaced from A(8, - 2, - 3) to B(-2, 0, 6) along the line segment AB, is
( A) 0
( B) 2
( C) 3.5
(D) 4.2
fl. If 8x - y = 15 is a tangent at (2, 1) to the curve y = x3 + a x2 + b , then (a, b) is
(A) (1, f)
(B) ( -1, f)
(C) (1, - f)
(D) ( -1, - f)
f2. The entire area bounded by the curve r2 = a Cos2G is
(A) a
(B) 2a
(C) n a
(D) 2n a
ff. The inverse of the matrix 1 O O O O"
1 1 O O O 1 O 1 O O 1 O O 1 O 1 O O O 1
is
l O O O O 1 -1 O O O 1 O -1 O O l O O -l O 1 O O O -1 1 O O O O -1 1 O O O 1 -1 O O O -1 O -1 O O 1 O O -1 O
1 O O O O -1 1 O O O -1 O 1 O O -1 O O 1 O -1 O O O 1
(A)
(B)
(C)
1 0 0 0 0
-1 1 0 0 0
(D)
-1 0 1 0 0
1 0 0 -1 0
1 0 0 0 -1
34. Suppose that 20 misprints are distributed randomly in a book of 900 pages. Assuming Poisson distribution, the probability that a chapter of 30 pages contains 2 misprints is
(A) 2 e-2/3 9
(B) - e-V2
9
-2/3
9
(C) 9 e 8
9 8 '
(D) - e~3/2
35. The double integral j j f (x, y) dydx under the transformation x = u (1 - v), y = uv
1 x
is transformed into
2/3 2/(1-v)
(A) j j f (u - uv, uv) dudv
1/2 1/(1-v)
2/3 2/(1-v)
(B) j j f (u - uv, uv) u dudv
1/2 1/(1-v)
2/3 2/(1-v)
(C) j j f (u - uv, uv) v dudv
1/2 1/(1-v)
1 2/(1-v)
(D) j j f (u - uv, uv) u dudv
2/3 1/(1-v)
36. If o is a non-real cube root of unity, then the eigenvalues of the matrix
|
1 > |
r 1 |
0 |
0 |
r1 |
1 |
1 | ||
|
CO2 |
0 |
-1 |
0 |
1 |
1/o |
1/o2 | ||
|
y |
V 0 |
0 |
0 y |
V1 |
1/o2 |
1/O4 y |
1 1 1
1 o coz
are
(A) 1, -1, 0
(B) 1 1 0
3 3
(C) 1, o, a>2
(D) 3, - 3, 0
37. The area bounded by the curve y = (x + 1)2, its tangent at (1, 4) and the x -axis is
(A) 3
(B) 3
(C) 1
4
3
(D)
38. Let V and Wbe vector spaces over a field F with dim FV = m and dim FW = n, where m and n both are finite. Then dimFHom(V,W) is
(A) m + n
(B) |m - n|
(C) mn
m
n
39. Which of the following is a unit normal vector to the surface z = xy at P (2, -1, -1) ?
(A)
- i + 2 j + k
(D)
V6
40. The nullity of the matrix
(1 - i 0 i i -1
0 2 - i - 2 2
- 2 - 4 3 - i - 3
1 + i 2 + i 1 2 i j
is
(A) 1
(B) 2
(C) 3
(D) 4
8 <-,3/2
(A) (103/2 +1) 27
(B) (103/2 -2) 27
(C) (103/2 -1) 27
(D) (103/2 + 2) 27
dx
42. The integral j
I x2(1 + ex)
(A) converges and has value < 1
(B) converges and has value equal to 1
(C) converges and has value >1
(D) diverges
43. Let (n, p) and X be the parameters of binomial and Poisson distributions respectively. Consider the statements
P. The mean of the binomial distribution is np
Q. The standard deviation of the binomial distribution is np(l-p)
R. The mean of the Poisson distribution is X
S. The variance of the Poisson distribution is X
Which of the following group of statements is correct?
(A) P, R, S
(B) P, Q, S
(C) P, Q, R
(D) P, Q, R, S
44. The order of the quotient group Z 8 x Z 9 x Z18 / < (2, 2, 2) ) is
(A) 18
(B) 36
(C) 72
(D) 144
45. Which of the following sets is NOT a convex set?
(A) {(x, y)| 4 x2 + y2 < 9, x - y < 1}
(B) {(x, y)| 4 x2 + y2 < 9, x - y > 1}
(C) {(x, y)| 4 x2 + y2 > 9, x - y > 5}
(D) {(x, y)| 4x2 + y2 > 9, x - y < 5}
1 .
z = is
2
<A) n
24
5n
(B)
12
| ||||||||||||||||||||||||||||||||||||
|
are linearly independent eigenvectors of M , then the main diagonal of the matrix B lMB has |
(A) exactly one real entry
(B) exactly two real entries
(C) exactly three real entries
(D) no real entry
48. The linear programming problem
Maximize z = 2x + 3y subject to
2x + 3y < 12
2 x - 3 y < 0
y < 2 x, y > 0
has
(A) no feasible solution
(B) unique optimal solution
(C) alternative optimal solutions
(D) unbounded solution
49. For the set W = { (x, 1, z) e IK.3}, consider the statements
P. W is not closed under vector addition Q. W is closed under scalar multiplication R. W has an additive identity
S. W is not a subspace of K3
Which of the following group of statements is true?
(A) P, R
(B) Q, R
(C) P, S
(D) Q, S
50. The number of values of A for which the system of equations
Ax + (A + 3) y = 10z (A-1) x + (A- 2) y = 5z
2 x + (A + 4) y = Az has infinitely many solutions, is
(A) 1
(B) 2
(C) 3
(D) infinite
2 1 1
51. Let A and B be events with P(A) = 3, P(B) = and P(A n B) = 3. Match lists
I and II and select the correct answer.
List I List II
1. P( A n Bc) P. 2
3
2. P( A u Bc) Q. 1
3
3. P(Ac nBc) R. -
6
4. P(Ac u Bc) S. 1
6
(A) (1, P), (2, Q), (3, R), (4, S)
(B) (1, R), (2, Q), (3, S), (4, P)
(C) (1, Q), (2, R), (3, S), (4, P)
(D) (1, Q), (2, R), (3, P), (4, S)
52. Consider the statements
(P) If a linear programming problem has only one optimal solution, then this solution is an extreme point of the feasible region.
(Q) A linear programming problem either is infeasible or has at least one optimal solution. (R) A linear programming problem can have exactly two optimal solutions.
(S) A feasible linear programming problem has an optimal solution or unbounded solution.
Which of the following group of statements is correct?
(A) P, Q
(B) P, R
(C) R, S
(D) P, S
53. For the linear programming problem
Minimize z = x - y
subject to
2 < x < 3
- 3 < y < 2
the minimum value of z is
(A) - 6
(B) - 5
(C) - 4
(D) 1
54. Let P be a set having n > 10 elements. The number of subsets of P having odd number of elements is
(A) 2n-1 -1
(B) 2n-1
(C) 2n-1 +1
(D) 2n -1
55. Let P be the set of all planes in IK.3. The relation being normal in P is
(A) symmetric and transitive
(B) symmetric and reflexive
(C) symmetric but not transitive
(D) transitive but not reflexive
56. For sets P, Q, R which of the following is NOT correct?
(A) (P u Q) n R = (P n R) u (Q n R)
(B) (P \ Q)\ R = (P \ R)\ (Q \ R)
(C) If P u Q = P u R, then Q = R
(D) P x (Q n R) = (P x Q) n (P x R)
57. If a b = a + b - ab for all a, b e R, then which of the following statements is correct?
(A) (R, ) is a group
(B) (R\{0}, ) is a group
(C) (R\{1}, ) is a group
(D) (R\{ -1}, ) is a group
58. (U x V) x W is equal to
(A) (U . W) V + (U . V) W
(B) (U . W) V - (V . W) U
(C) (V . W) U - (U . W) V
(D) (U . W) V + (V . W) U
59. The addition of the BCD numbers given below
01100111 and 01010011
is
(A) 000100100000
(b) 000110100000
(c) 000101100000
(d) 000101010000
60. The output of the following program main( )
{ int a[ ] = { 2,3,4,6,5}; int *p = a;
for (int i = 0; i < 5; i++) printf(%d,,++*p);
}
is
(A) 3, 4, 5, 6, 7
(B) 3, 4, 5, 7, 6
(C) 3, 4, 6, 5, 0
(D) 3, 4, 5, 6, 6
61. The multiplication of numbers (47)8 and (52)8 is
(A) (3144)8
(B) (3146)8
(C) (4147)8
(D) (4146)8
62. The output of the following program
main( )
{ int a = 10; b = 4; if(a&1 || b&1) printf(Hello); else printf(Welcome);
}
is
(A) Hello
(B) WelcomeHello
(C) HelloWelcome
(D) Welcome
63. The sequence 10000, 121, 100, 31, 24,_, 20 represent a number x with respect
to different bases. The missing number in this sequence is
(A) 22
(B) 21
(C) 16
(D) 10
64. The program
main( )
{ int a = 256, *p=&a; printf(%d,*p>>5);
}
prints
(A) 2
(B) 4
(C) 6
(D) 8
65. If (41)6 = (121)b then b is
(A) 1
(B) 2
(C) 3
(D) 4
66. The output of the following program
main( )
{
int a[ ] = computation; char *p = a, b= ; for (int i = 1; i < 12; i++) if(i%4) continue; else a[i]=b; puts(p);
}
is
(A) comp
(B) comp tat on
(C) com utat on
(D) comp tati n
(an/2)2, n even
otherwise
then to compute a27, the minimum number of multiplications and squaring required respectively are
(A) 3 and 4
(B) 4 and 3
(C) 27 and 14
(D) 26 and 13
The output of the following logic circuit diagram for x = 0, y = 1, z = 1, u = 0,
v = 1, w = 0
aa
68.
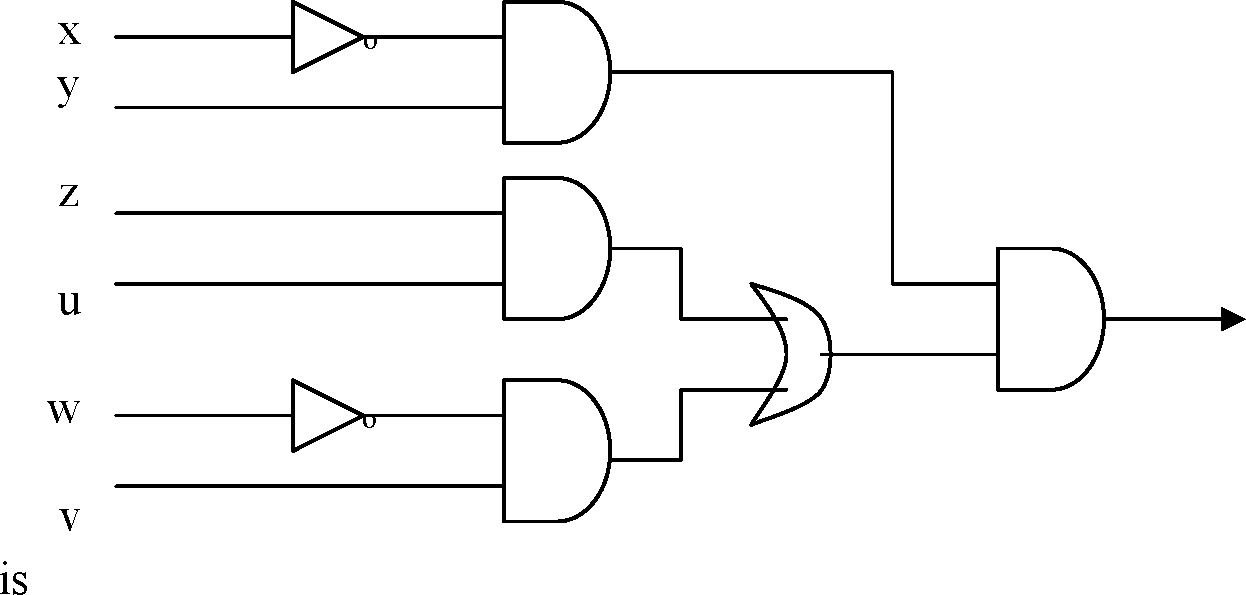
(A) 0
(B) 00
(C) 1
(D) 10
69. The following function computes int f(int p)
{
static int x = 10;
if(x = = 1) return 1; if(x > 0)
{ x--; return p*f(p);
}
}
(A) p9
(B) p10
70. Which of the following combinations is invalid in SR flip-flops?
(A) S = 0, R = 0
(B) S = 0, R = 1
( C) S = 1, R = 0
(D) S = 1, R = 1
71. What does the following function return ?
int f( )
{
int a, b, c; if(a > b) if(a > c)
if(c > b) return c;
else return b; else return a; else if(c > a) if(c > b) return b; else return c; else return a;
}
(A) minimum(a, b, c)
(B) maximum(a, b, c)
( C) middle(a, b, c)
(D) gcd(a, b, c)
72. What does the following function print?
void f( )
{
char p;
if((p = getchar()) != \n) f( );
putchar(p);
return;
}
(A) reverse of the given characters
(B) characters in the given order
(C) characters in the given order without the first character
(D) reverse of the given characters without the last character
73. The output of the following program
main( )
{
int i = 4, j = 5; while(i <= 6)
{
if(j >= 100) j = j - 2; else j = i*j; j++; i++;
}
printf(%d, %d, i++, j);
}
is
(A) 6, 105
(B) 6, 106
(C) 7, 105
(D) 7, 106
74. What is the output of the following program?
main( )
{
int a, b, *p1, *p2, y; a = 3; b = 4; p1 = &a; p2 = &b;
y = 4*-*p2/ *p1+10;
a* = b* = a* = y; printf(%d,%d,%d,y,a,b);
}
(A) 5, 60, 900
(B) 5, 900, 60
(C) 60, 900, 5
(D) 900, 60, 5
75. From the following flip-flops JK flip-flop
P. SR flip-flop Q. D flip-flop R. T flip-flop
The pair of flip-flops which uses only one input is
(A) (P, S)
(B) (Q, R)
(C) (R, S)
(D) (P, R)
List I P. optical memory Q. ADA R. Unix
S. memory stick
List II
1. operating system
2. USB port
3. programming language
4. CD-ROM
(A) (P, 4), (Q, 3), (R, 1), (S, 2)
(B) (P, 3), (Q, 2), (R, 4), (S, 1)
(C) (P, 2), (Q, 1), (R, 3), (S, 4)
(D) (P, 1), (Q, 4), (R, 2), (S, 3)
77. ASCII stands for
(A) American Standard Code for International Interchange
(B) American Scientific Code for Information Interchange
(C) American Standard Code for Intelligence Interchange
(D) American Standard Code for Information Interchange
78. Match list I and list II and select the correct group of matching
List I P. Wolfram
List II
1. LISP
2. C++
3. C
4. MATHEMATICA
Q. Kennighnan & Ritchie R. John McCarthy S. Stroustrup
(A) (P, 1), (Q, 2), (R, 3), (S, 4)
(B) (P, 2), (Q, 3), (R, 4), (S, 1)
(C) (P, 3), (Q, 4), (R, 1), (S, 2)
(D) (P, 4), (Q, 3), (R, 1), (S, 2)
79. Consider the following pseudo code
1. for i 1 to 9
2. x = 1
3. for j i to 10
4. y = 2
The number of times the statement 2 and statement 4 executed respectively are
(A) (9, 9)
(B) (9, 54)
(C) (9, 90)
(D) (10, 54)
80. Consider a tri-diagonal matrix A = (aij)n x n . If the diagonal elements are stored in a linear array B as B[1] = a11, B[2] = a12, B[3] = a13, B[4] = a22, ... , then the relation in terms of m, k and l such that B[m] = a is
(A) m = k + l -2
(B) m = 2 k -1 +2
(C) m = 2 k + l -2
(D) m = k + 2 l -1
81. Match list I and list II and select the correct group of matching
List I List II
P. RAM 1. Hz
Q. CPU speed 2. MB
R. Monitor 3. Bytes/sec.
S. CD-ROM speed 4. inch
(A) (P, 2), (Q, 1), (R, 4), (S, 3)
(B) (P, 1), (Q, 2), (R, 3), (S, 4)
(C) (P, 3), (Q, 4), (R, 2), (S, 1)
(D) (P, 4), (Q, 3), (R, 1), (S, 2)
82. Which of the following is NOT a language processor?
(A) compiler
(B) loader
(C) interpreter
(D) assembler
83. Which of the following is NOT a internet protocol?
(A) LTP
(b) SMTP
(C) HTTP
(D) ATM
84. Which of the following statements in a Boolean algebra is NOT correct?
(A) A + A = A
(B) A . A = A
(C) A + 1 = A
(d) A + AB = A
85. Which of the following statements in a Boolean algebra is correct?
(A) AB = A + b
(B) AB = A . B
(C) AB = A + B
(D) AB = A + B
86. The sequence that is in ascending order in size is
(A) bit, word, byte, nibble
(B) nibble, byte, bit, word
(C) nibble, bit, word, byte
(D) bit, nibble, byte, word
87. INDIA became Sovereign Democratic Republic country on
(A) 1950, January 26
(B) 1948, January 26
(C) 1947, August 15
(D) 1952, January 26
88. In the following table, numbers 1, 2, 3, 4 are to be arranged wherever missing in such a way that each row as well as each column has all of these numbers exactly once
|
4 |
2 | ||
|
2 |
4 | ||
|
1 | |||
|
1 |
The missing entries in the main diagonal are
(A) 1, 2, 3
(B) 2, 3, 4
(C) 1, 3, 4
(D) 1, 2, 4
89. If the word MANMOHANWASHERE corresponds to
ZOAABVNBJOFVRFR, then the word that corresponds to LRF is
(A) HEY
(B) MAN
(C) GOT
(D) YES
3
11
6 :
25
12
137
60
90. The next term in the sequence 1,
is
2
2_
10
299
120
151
60
49
20
(A)
(B)
(C)
(D)
91. The Headquarter of UNO is based in the city
(A) Geneva
(B) London
(C) Moscow
(D) New York
List I
P. Abhijnana Shakuntalam Q. Godan
1. Tulsidas
2. Valmiki
3. Kalidas
4. Jawaharlal Nehru
5. Prem Chand
R. Ramcharitmanas S. Ramayana T. Discovery of India
Which of the following group is correct ?
(A) (R-2, S-3, T-4)
(B) (P-1, Q-5, S-2)
(C) (P-3, S-2, T-4)
(D) (Q-5, R-2, T-4)
93. In 2004 Olympic Games, Rajyavardhan Singh Rathore won
(A) Gold Medal
(B) Silver Medal
(C) Bronze Medal
(D) No Medal
94. A man has to travel from a point P to a point Q, 256 km apart. He travels half the distance on day one, half of the remaining distance on day two, half of the remaining distance on day three and so on. He reaches exactly at the point Q
(A) in 8 days
(B) in 16 days
(C) in 24 days
(D) never
95. A pipe can fill an empty tank in 6 hours, while another pipe can empty the full tank in 8 hours. If both the pipes are opened together when the tank is half full, then the tank will be full in
(A) 6 hours
(B) 12 hours
(C) 18 hours
(D) 20 hours
96. Total number of ways in which four boys and three girls can sit in a row so that boys and girls have alternate seats is
(A) 72
(B) 144
(C) 288
(D) 720
97. Consider the following statements
Ram eats if he is hungry If Ram eats, then he will sleep
which of the following is true ?
(A) Ram is sleeping, he ate
(B) Ram did not eat, he is not sleeping
(C) Ram ate, he is not hungry
(D) Ram is not sleeping, he did not eat
98. Let there be six distinct points in a plane. The maximum number of polygons having these points as their only vertices is
(A) 24
(B) 42
(C) 64
(D) 84
99. In the context of Internet, WWW stands for
(A) Wireless World Web
(B) World Wise Web
(C) Wide Wireless Web
(D) World Wide Web
100. Match list I and list II and select the correct answer
List I
List II
1. Microsoft
2. Wipro
3. Satyam
4. Infosys
P. Azim Premji
Q. Narayana Murthy
R. Bill Gates
S. Ramalinga Raju
(A) (P, 1), (Q, 2), (R, 3), (S, 4)
(B) (P, 2), (Q, 3), (R, 4), (S, 1)
(C) (P, 3), (Q, 1), (R, 2), (S, 4)
(D) (P, 2), (Q, 4), (R, 1), (S, 3)
25
|
Attachment: |
| Earning: Approval pending. |
