Indian Institute of Technology Guwahati (IIT-G) 2005 JAM Physics - Question Paper
JAM 2005 Physics
Full ques. Paper in attachment
|
2005 - PH A
2005 - PH READ THE INSTRUCTIONS ON THE LEFT SIDE OF THIS PAGE CAREFULLY Test Paper Code : PH Time : 3 Hours Max. Marks : 300 INSTRUCTIONS 1. The question-cum-answer book has 32 pages and has 25 questions. Please ensure that the copy of the question-cum-answer book you have received contains all the questions. 2. Write your Roll Number, Name and the name of the Test Centre in the appropriate space provided on the right side. 3. Write the answers to the objective questions against each Question No. in the Answer Table for Objective Questions, provided on page No. 7. Do not write anything else on this page. 4. Each objective question has 4 choices for its answer: (A), (B), (C) and (D). Only ONE of them is the correct answer. There will be negative marking for wrong answers to objective questions. The following marking scheme for objective questions shall be used : (a) For each objective question, you will be awarded 6 (six) marks if you have written only the correct answer. Do not write your Roll Number or Name anywhere else in this question-cum-answer book. (b) In case you have not written any answer for a question you will be awarded 0 (zero) mark for that question. (c) In all other cases, you will be awarded -2 (minus two) marks for the question. I have read all the instructions and shall abide by them. 5. Answer the subjective question only in the space provided after each question. 6. Do not write more than one answer for the same question. In case you attempt a subjective question more than once, please cancel the answer(s) you consider wrong. Otherwise, the answer appearing later only will be evaluated. Signature of the Candidate 7. All answers must be written in blue/ black/blue-black ink only. Sketch pen, pencil or ink of any other colour should not be used. 8. All rough work should be done in the space provided and scored out finally. 9. No supplementary sheets will be provided to the candidates. I have verified the information filled by the Candidate above. 10.Logarithmic Tables / Calculator of any kind / cellular phone / pager / electronic gadgets are not allowed. 11.The question-cum-answer book must be returned in its entirety to the Invigilator before leaving the examination hall. Do not remove any page from this book. Signature of the Invigilator 12.Refer to useful data on the reverse. |
| ||||||||||||||||
|
INSTRUCTIONS : | |
|
1. |
Attempt ALL the 25 questions. Questions 1-15 (objective questions) carry six marks each and questions 16-25 (subjective questions) carrv twenty one marks each. |
|
2. |
Write the answers to the objective questions ONLY in the Answer Table for Objective Questions provided on page 7. |
|
3. |
The answers obtained in terms of logarithms, irrational numbers and fundamental constants need not be simplified any further. |
|
4. |
The final answers can be left as a ratio or product of two numbers without further simplification. |
|
5. |
Mention units wherever applicable. |
1. A solid sphere of mass m and radius a is rolling with a linear speed v on a flat surface without slipping. The magnitude of the angular momentum of the sphere with respect to a point along the path of the sphere on the surface is
/ A \ 2
(A) mav 5
7
(B) mav 5
(C) mav
(D) mav 2
2. The susceptibility of a diamagnetic material is
(A) positive and proportional to temperature
(B) negative and inversely proportional to temperature
(C) negative and independent of temperature
(D) positive and inversely proportional to temperature
5
3. The molar specific heat of a gas as given from the kinetic theory is R . If it is not specified
2
whether it is Cp or Cv, one could conclude that the molecules of the gas
(A) are definitely monatomic
(B) are definitely rigid diatomic
(C) are definitely non-rigid diatomic
(D) can be monatomic or rigid diatomic
4. The value of entropy at absolute zero of temperature would be
(A) zero for all the materials
(B) finite for all the materials
(C) zero for some materials and non-zero for others
(D) unpredictable for any material
5. A circuit and the signal applied at its input terminals (V) are shown in figure below. Which one of the options correctly describes the output waveform (V0). (Assume all the devices used are ideal).
+2 V
c
A D
Vi
Vo
> t
0
-2 V
2 V
(A)
(B)
-2 V
-2 V
(C)
|
4 V |  |
A
Consider a beam of light of wavelength X incident on a system of a polarizer and an analyzer. The analyzer is oriented at 45 to the polarizer. When an optical component is introduced between them, the output intensity becomes zero. (Light is incident normally on all components). The optical component is
(A) a full-wave plate
(B) a half-wave plate
(C) a quarter-wave plate
(D) an ordinary glass plate
A small loop of wire of area A = 0.01 m2 , N = 40 turns and resistance R = 20 2 is initially kept in a uniform magnetic field B in such a way that the field is normal to the plane of the loop. When it is pulled out of the magnetic field, a total charge of Q = 2xlO~5C flows through the coil. The magnitude of the field B is
(A) 1 x 10'3 T
(B) 4 x 10~3T
(C) zero
(D) unobtainable, as the data is insufficient
If Me, Mp and MH are the rest masses of electron, proton and hydrogen atom in the
ground state (with energy -13.6 eV), respectively, which of the following is exactly true? (c is the speed of light in free space)
(A) Mh =Mp + Me
/T->\ TV/r TVT TV/r 13.6 eV
(B) Mh =M +Me--i
c
m A/r n/r a/t 13.6 eV
(C) Mh M + M h---
c2,
-J Q \J
(D) Mh =Mp +Me + K, where K or zero
9. An observer is sitting on a horizontal platform which is rotating with a constant angular velocity. He puts an object on the smooth frictionless floor of the platform, away from the axis of rotation, with zero initial velocity with respect to him. Let the time at this instant be t - 0 . In the frame of the platform, the object would
|
(A) |
remain at rest for all t > 0 | |
|
(B) |
accelerate purely in a radial direction outwards for all t > 0 | |
|
(C) |
accelerate purely in a tangential direction for all t > 0 | |
|
(D) |
accelerate radially in the outward direction at t - 0, acceleration changes for t > 0 |
however the direction of |
|
(0 Which of the following is INCORRECT for the matrix M = |
'V 0) | |
|
(A) |
It is its own inverse | |
|
(B) |
It is its own transpose | |
|
(C) |
It is non-orthogonal | |
|
(D) |
It has eigen values 1 | |
11. A combination of two thin convex lenses of equal focal lengths, is kept separated along the optic axes by a distance of 20 cm between them. The combination behaves as a lens system of infinite focal length. If an object is kept at 10 cm from the first lens, its image will be formed on the other side at a distance x from the second lens. The value of is
|
(A) |
10 cm |
|
(B) |
20 cm |
|
(C) |
6.67 cm |
|
(D) |
infinite |
12. Two point charges +q1 and +q2 are fixed with a finite distance d between them. It is desired to put a third charge q3 in between these two charges on the line joining them so that the charge q3 is in equilibrium. This is
(A) possible only if q3 is positive
(B) possible only if q3 is negative
(C) possible irrespective of the sign of q3
(D) not possible at all
13. A periodic function can be expressed in a Fourier series of the form, fix) = (an cos inx) + bn sin inx)). The functions fix) = cos2x and f2ix) - sin2 x are
n=0
expanded in their respective Fourier series. If the coefficients for the first series are and &1), and the coefficients for the second series are a2) and b{\ respectively, then which of the following is correct?
(A) a{2] = and b22) = -
2 2
(B) =- and af1 =
2 2
(C) = and ag2) 1 -
1 2 2
(D) = i and 62) =
* 2 2
14. Which of the following statements is correct for NaCl crystal structure?
(A) It is a simple cubic lattice with one atom basis
(B) It is a face-centered cubic lattice with one atom basis
(C) It is a simple cubic lattice with two atom basis
(D) It is a face-centered cubic lattice with two atom basis
15. Which of the following statements is INCORRECT ?
(A) Indistinguishable particles obey Maxwell-Boltzmann statistics
(B) All particles of an ideal Bose gas occupy a single energy state at T = 0
(C) The integral spin particles obey Bose-Einstein statistics
(D) Protons obey Fermi-Dirac statistics
16. (a) Consider a constant vector field v = v0k . Find any one of the many possible vectors u , for which V xu = u .
(b) Using Stokes theorem, evaluate the flux associated with the field v through the curved hemispherical surface defined by x2 + y2 + z2 = r2, z >0.
17. A logic circuit and the time varying logic levels applied at its A and B inputs are shown below. Sketch the corresponding output waveform at points C, D, E, F and G in the space given below the waveforms A and B.
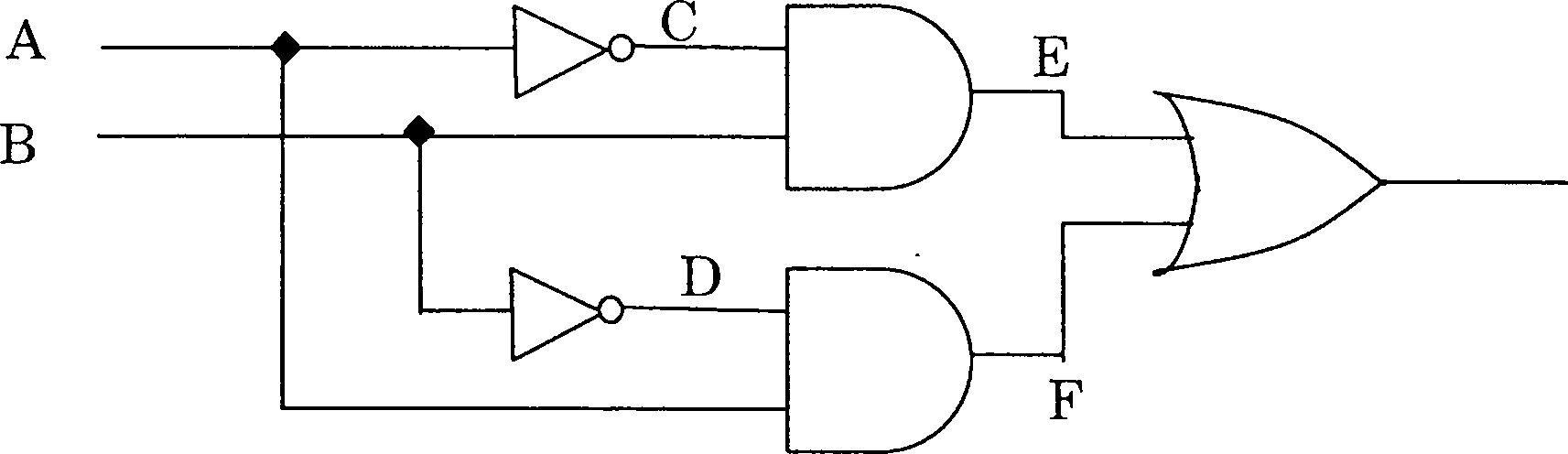 |
G |
l
1
1
l
E o


18. (a) Determine whether the force represented by Fix, y) = k [(x2 + y2) i + 2xy j\ is conservative or not. Here k = 1 Nm'2.
(b) Calculate the work done by this force in moving a particle from the origin 0(0,0,0) to the point D(1,1,0) on the z - 0 plane along the paths OABD and OD as shown in the figure, where the coordinates are measured in metres.
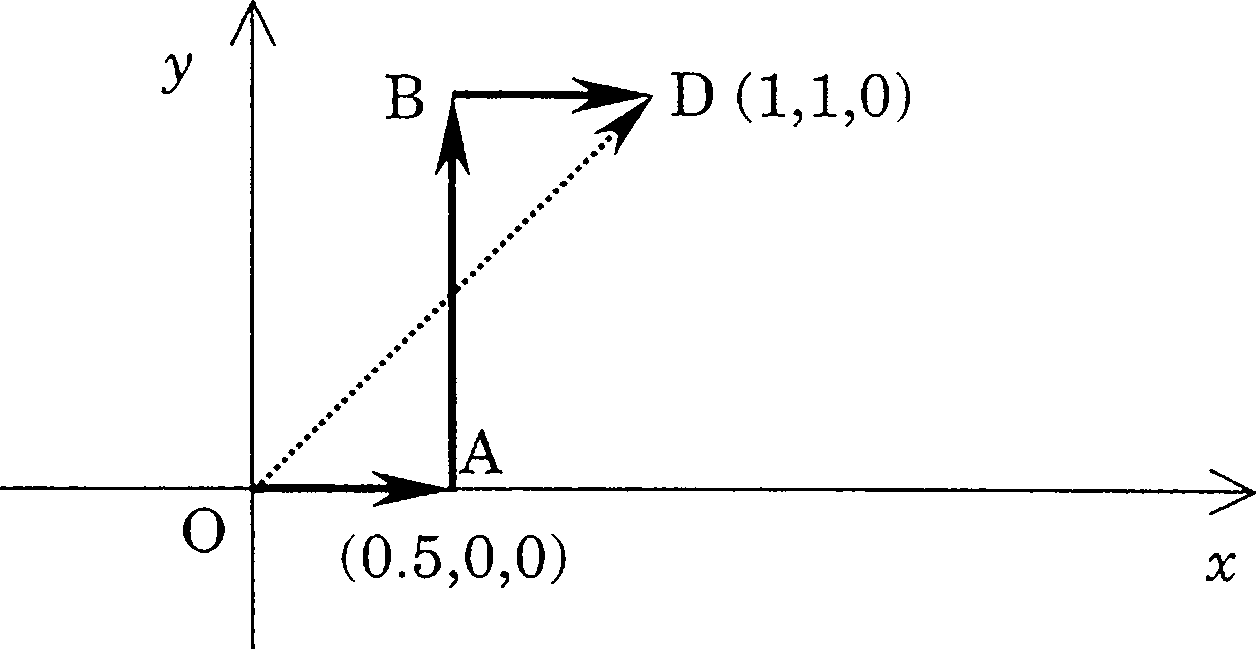
19. A rod is moving with a speed of 0.4 c along its length in the positive x-direction, and a particle is moving along the negative x-direction with a speed 0.8 c as shown in the figure below. Both the speeds are measured in an inertial frame S, and c is the velocity of light in free space. The length of the rod as measured in the S-frame is 3.6 m.
(a) Find the relative velocity of the rod (in terms of c) in the rest frame of the particle.
(b) Find (i) the time taken for the particle to cross the rod in the S-frame and in the rest frame of the rod, and (ii) time taken by the rod to cross the particle in the rest frame of the particle.
0.8 c <-
A
A particle of mass m and energy E, moving in the positive x-direction, encounters a onedimensional potential barrier at x = 0 . The barrier is defined by
V = 0 for x < 0
V = V0 for x > 0 (V0 is positive and E >V0)
If the wave function of the particle in the region x < 0 is given as A elkx + B e~lkx ,
(a) Find the ratio .
A
B E
(b) If = 0.4, find , and the transmission and reflection coefficients.
21. (a) Establish the equation dU - | dT +
) -P IdTjy
dV, given that
bp
as
ay
= j | , where U, P, T, V and S are, respectively, the
dU = TdS - PdV and
internal energy, pressure, temperature, volume and entropy of the system.
(b) If the specific heat is taken to be independent of T, utilize the above equation to derive an expression for U(T, V) for one mole of a van der Waals gas and then obtain
the corresponding expression for an ideal gas.
22. Solve the differential equation xy = 3y2 +x2 with the initial condition y = 2 when
dx
x = 1.
A beam of light is incident normally on a diffraction grating of width 2 cm. It is found that at 30, the /2 th order diffraction maximum for A1 - 5000 is super-imposed on the (n + l)th order for A2 = 4000 A. How many lines per cm does the grating have? Find out whether the first order spectrum from such a grating can be used to resolve the wavelengths A3 = 5800 and A4 = 5802 ?
Consider two electromagnetic plane waves propagating in vacuum with their electric field
A A
vectors Ex - E0 cos{kz - ot)i and E2 = E0 cos{kz + ot)i.
(a) Evaluate the magnetic field vector corresponding to the superposition of these two waves.
(b) Calculate the time-averaged energy density as well as the time-averaged Poynting vector for the resultant wave. (The time average is carried over one period of oscillation).
A 150 Q resistor, a 10 |iF capacitor and a 0.1 H inductor are connected in series to an a.c.
source operating at an angular frequency co.
(a) Find the value of co for which the combination acts as a pure resistive load.
(b) The a.c. source is operated at a peak voltage of 3002 V and a frequency equal to half the resonance frequency of the circuit. Find the peak value of the current in the circuit and the phase difference between the current and voltage. Also, find the peak voltage across the inductor.

|
Attachment: |
| Earning: Approval pending. |

