Indian Institute of Technology Guwahati (IIT-G) 2005 JAM MATHS - Question Paper
JAM 2005 MATHS
IMPORTANT NOTE FOR CANDIDATES
Objective Part :
Attempt ALL the objective questions (Questions 1 - 15). Each of these questions carries six marks. Write the answers to the objective questions ONLY in the Answer Table for Objective Questions provided on page 7.
Subjective Part :
Attempt ALL questions in the Core Section (Questions 16 - 22). Questions 16 - 21 carry twenty one marks each and Question 22 carries twelve marks. There are Five Optional Sections (A, B, C, D and E). Each Optional Section has two questions, each of the questions carries eighteen marks. Attempt both questions from any two Optional Sections. Thus in the Subjective Part, attempt a total of
11 questions.
cL v cJi/v
3. The general solution of x2 - - 5x--h 9y = 0 is
dx2 dx
(A) (cj + c2x)e3x
(B) (cj + c2 Inx)x3
(C) (cj + c2x)x3
(D) (cj + c2 In x)ex
(Here cx and c2 are arbitrary constants.)
4. Let r = xi + ;yj+zk. If 0{x,y,z) is a solution of the Laplace equation then the vector field
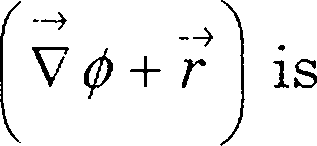
(A) neither solenoidal nor irrotational
(B) solenoidal but not irrotational
(C) both solenoidal and irrotational
(D) irrotational but not solenoidal
5. Let F = x i+ 2y j+ 3z k, S be the surface of the sphere x2 + y2 + z2 =1 and n be the
inward unit normal vector to 5 . Then J*J* ndS is equal to
s
(A) 4 n
(B) -4 n
(C) 8 n
(D)
A
(A) A2 + A is non-singular
(B) A2 - A is non-singular
(C) A2 +3A is non-singular
(D) A2 -3A is non-singular
Let T : R3-> R3 be a linear transformation and I be the identity transformation of R3.
If there is a scalar c and a non-zero vector x e R3 such that T(x) = cx, then rank(T - cl)
(A) cannot be 0
(B) cannot be 1
(C) cannot be 2
(D) cannot be 3
In the group {l, 2, ..., 16} under the operation of multiplication modulo 17, the order of the element 3 is
(A) 4
(B) 8
(C) 12
(D) 16
A ring R has maximal ideals
(A) if R is infinite
(B) if R is finite
(C) if R is finite with at least 2 elements
(D) only if R is finite
dy
dy
dy
dy
jo |_ jo V.J0 2 r f2 / rl-y
(d> r r r**
u
11. Let f : R-> R be continuous and g, h : R2-> R be differentiable. Let F(u,v) = j* f(t)dt,
d F dF
where u = g (x,y) and v = h (x,y). Then -+-
d x d y
dg , dg dx d y
dg [ dg dx dy
dg , dg dx dy
dh_ dh_ dx dy
- f (h(x,y)) + f(g(x,y))
+ f(g(x,y))
dh_rk
dx dy
dh_dh dx dy
dhL_dhL dx dy
dg dg dx dy
|
(A) |
f(g(x,y)) |
|
(B) |
f(h(x,y)) |
|
(C) |
f(h(x,y)) |
|
(D) |
f(g(x,y)) |
12. Let y = f (x) be a smooth curve such that 0 < f(x) < K for all x e \a,b\. Let L = length of the curve between x = a and x = b
A = area bounded by the curve, x -axis, and the lines x = a and x = b
S = area of the surface generated by revolving the curve about x -axis between x = a and x = b
Then
(A) 2ttKL <S < A
(B) S < 2nA < 2ttKL
13. Let f: R-> R be defined by f(t) = t2 and let U be any non-empty open subset of JR.
Then
(A) f(U) is open
(B) f~\U) is open
(C) f(U) is closed
(D) f~\U) is closed
14. Let f : (-1,1) -> R be such that f'l\x) exists and | /(x)| < 1 for every n > 1 and for
every xg (-1,1). Then f has a convergent power series expansion in a neighbourhood of
(A) every ig (-1,1)
(B) every xe only
(C) no x (-1,1)
(D) every xe 0, only
15. Let a > 1 and f,g,h: \-a, a] -> R be twice differentiable functions such that for some c
with 0 < c < 1 < a ,
f (x) = 0 only for x = -a, 0, a ; f\x) = 0 = g (x) only x = -1, 0,1 ; g'(x) = 0 = h (x) only for x = -c, c .
The possible relations between f, g, h are
(A) f - g and h = f'
(B) f' = g and g = h
(C) f = -g' and h' = g
(D) f = -g' and h' = f
CORE SECTION
16. (a) Solve the initial value problem d2y
. .,~y =*(sinx + e*), 3,(0) = /(0) = l (12)
dx
(b) Solve the differential equation
(2ysinx+ 3y4sinx cosx)dx - (43/3cos2x + cosx)dy = 0
Let G be a finite abelian group of order n with identity e. If for all a e G, a3 =e, then, by induction on n, show that n = Sk for some nonnegative integer k. (21)
18. (a) Let f \\a,b]> R be a differentiable function. Show that there exist points cl5 c2 G (a,b) such that
(9)
(b) Let
(x2 +y2)[\n(x2 +y2)+l] for (x,y)*(0,0)
f(x,y) = -S
for (x,y) =(0,0)
a
Find a suitable value for a such that f is continuous. For this value of a, is f differentiable at (0,0) ? Justify your claim. (12)
19. (a) Let S be the surface x2 + y2 + z2 = 1, 2 > 0 . Use Stoke's theorem to evaluate
j* \(2x - y)dx - ydy - zdz] c
where C is the circle x2 + y2 = 1, z = 0, oriented anticlockwise. (12)
(b) Show that the vector field F = (2xy -y4 +3)i + (x2 -4xy3 )j is conservative. Find its potential and also the work done in moving a particle from (1,0) to (2,1) along some curve. (9)
Let T : R3->R3 be defined by T(x,y,z) = (y + z,z,0). Show that T is a linear
transformation. If v R3 is such that T2(v)0, then show that B = {v, T(v), T2 (v)} forms a basis of R3. Compute the matrix of T with respect to B. Also find a v e R3 such that T2(v) 0. (21)
4 n x
fnW
4n \x
n
0, 2 n
J_ j.
2n n
1
, 1
n
l
Compute ftl{x)dx for each n. Analyse pointwise and uniform convergence of the
sequence of functions {fn }.
(12)
(b) Let f: R > R be a continuous function with |/'()-/'(3;)||x-j| for every x,y G R . Is f one-one? Show that there cannot exist three points a, b, c g R with a <b < c such that f(a) < fic) < fib). (9)
Find the volume of the cylinder with base as the disk of unit radius in the xy -plane centred at (1, 1, 0) and the top being the surface z = [(x-l)2 + (y-l)2] . (12)
23. (a) Bag A contains 3 white and 4 red balls, and bag B contains 6 white and 3 red balls.
A biased coin, twice as likely to come up heads as tails, is tossed once. If it shows head, a ball is drawn from bag A, otherwise, from bag B. Given that a white ball was drawn, what is the probability that the coin came up tail? (9)
(b) Let the random variables X and Y have the joint probability density function f(x,y) given by
f(x, y) =
Are the random variables X and Y independent? Justify your answer.
(9)
24. (a) Let XY, X2, ..., Xn be independently identically distributed random variables (rv's)
with common probability density function (pdf) fx (x,6) = e~x/0; x > 0, 6 > 0. Obtain
0
_ 1 n
the moment generating function (mgf) of X = / Xt. Also find the mgf of the rv
Y = 2nX/0. (9)
(b) Let Xx, X2, ..., X9 be an independent random sample from (2,4) and Ylf Y2, Y3, Y4 be an independent random sample from N (1,1). Find P(x >Y), where X and Y are sample means.
[Given P(Z > 1.2) = 0.1151, where Z ~ N(0,1)] (9)
25. (a) Let Xx, X2, ..., Xn be a random sample from a distribution having pdf
ax,
for x > x,
. a+1
f(x;x0,a) =
x
0 otherwise
where x0 > 0, a > 0. Find the maximum likelihood estimator of a if x0 is known. (9)
(b) Let X1, X2, ..., X5 be a random sample from the standard normal population. Determine the constant c such that the random variable
c(X1 +X2)
Y
will have a -distribution.
(9)
26. (a) A random sample of size n = 1 is drawn from pdf fx (x,0) = > 0, (9 > 0 . It is
decided to test HQ : 6 = 5 against Hx : 0 = 7 based on the criterion: reject 7/0 if the observed value is greater than 10. Obtain the probabilities of type I and type II errors. (9)
(b) Let X1} X2 ? ..., Xn be a random sample from a normal population n(ju, a2). Find the best test for testing H0 : // = 0, a2 =1 against Hl : ju = 1, cf2 = 4 . (9)
27. (a) Let f,g:R-> R be such that for x,y& R,
<p(x+iy) = ex\f(y) + ig(y)\ is an analytic function. Find a differential equation of order 2 satisfied by f. (9)
(b) Compute I* (2z + l)e2 + l'z dz. (9)
JI z-fl1=2
28. (a) Let f(z) be analytic in the whole complex plane such that for all r > 0,
2 n
| l/tre')! d6 < 4r
o
Find -- for all n > 0. (9)
n!
(b) Find all values of aeC such that f(z) = (z +z)2 +2a\z |2 + a(z)2 is analytic at some point 2 having non-zero real part. (9)
A hemispherical bowl of radius 12 cm is fixed such that its rim is horizontal. A light rod of length 20 cm with weights w and W attached to its two ends is placed inside the bowl. In equilibrium, the weight w is just touching the rim of the bowl. Find the ratio w : W. (18)
A uniform ladder of length 2a and mass m lies in a vertical plane with one end against a smooth wall, the other end being supported on a horizontal floor. The ladder is released from rest when inclined at an angle a to the horizontal. Find the inclination of the ladder to the horizontal when it ceases to touch the wall. (18)
R
31. (a) Estimate the error in evaluating the integral J(l + x2)e~xdx by Simpson's rd rule
o
with spacing h = 0.25. (9)
(b) Using Newton-Raphson method, compute the point of intersection of the curves y = x3 and y = 8x + 4 near the point x = 3, correct up to 2 decimal places.
[Round-off the first iteration up to 2 decimal places for further computation] (9)
The polynomial p3(x) = x3 + x2 - 2 interpolates the function fix) at the points
x = -1, 0, 1 and 2. If the data /(3) = -14 is added, find the new interpolating polynomial
by using Newton's forward difference formula. Also find f{2.5) by using Newton's
backward difference formula with pivot value 3. Justify whether the value obtained will be the same if pivot value 2 is taken. (18)
o
|
Attachment: |
| Earning: Approval pending. |

