Bharathiar University 2008 B.A Tamil -1 - Question Paper
click the beneath link to download the pdf file
Reg. No.:.........................................
D 3152 Q.P. Code : [DT 107/
Reg. No.:.........................................
DT 1 C 07]
(For the candidates admitted from 2007 onwards) U.G. DEGREE EXAMINATION, JUNE 2008.
First Year I
prror I QsiuiLjen LDipgju} e_a>i7fl>er>u Time : Three hours Maximum : 100 marks
rer>aj(5ujg)ftb fgrisfri 6uiq.6fily ettau
Reg. No.:.........................................
(5 x 20 100)
1. urrijuSlar *65i6i| urrpCib &gS)t> L|a>uu6iiJg> 6fi)6uifl.
2. uni)$fT*0T 6fi)r> B_jT(VgjLh fT)Lh rbitil $ rl-soe; u
3. $)UiSla>rT uDfTOTTLjSCTT ajntnoj?
4. erefila&GCTU-iGfli-aftio Q$iu$*>6n
$yjfnu.
6. Quiflujmflor siflfTio Qarrenaaa @r$)$$} cr(tpi*.
7. CSn.p. s>r$0rru5) Snfpiih uwrunil.u}.n6CT 6filnft(ff>a.
8. $)lUfTU>fi>JD 6U$UIT - 6filGT*@*.
(For the candidates admitted from 2007 onwards) U.G. DEGREE EXAMINATION, JUNE 2008.
First Year Part II English ENGLISH-I
Time : Three hours Maximum : 100 marks
Answer any FIVE of the following.
Choose any FIVE out of the eight questions given.
All questions carry equal marks.
(5 x 20 =100) Answer the following each in about 400 words.
1. How did the selfish giant find his way to heaven?
2. What impressions do you form of Lalajee and Jim Corbett from Corbetts account?
3. How does Mansfield bring out his belief that happiness is the essence of life?
4. Attempt a critical appreciation of Wordsworths Lucy Gray.
5. Sketch the character of Shylock from your reading of the trial scene.
6. Examine the appropriateness of the title, The Eves Are not There.
7. Answer any FOUR in about 100 words each.
(a) Why did the model for Judas Iscariot become increasingly agitated as the portrait developed?
(b) Describe Midas' second meeting with the stranger.
(c) How did Matilda fall a victim to her infirmity of telling dreadful lies?
(d) He knelt him at that word. Account for Peter Gilligans gesture.
(e) What is the central theme of The Informer?
(f) Account for the fear of death of Schatz.
(a) We believe him
(Change into (i) Negative and (ii) Question)
(b) She hasn't spoken to me.....
(Complete the sentence with (i) more than two years (ii) last week)
(c) We _ (walk) to the station
when it___(begin) to rain
(Pill in the blanks with suitable forms of the verb given in the bracket)
(d) (i) He is a best friend of mine.
(ii) I shall call on him when he will come (Correct the sentences, if necessary)
(e) (i) They have made my brother the captain.
(ii) Poverty drove him to desperation. (Change into passive voice)
(f) Who has dared to wound you, cried the giant, tell me, that I may take my big sword and slay him
(Change into reported speech)
(g) My wife never agrees _
me_anything
(Pill in the blanks with suitable prepositions)
(h) He is_ honourable man
He is_one-eyed beggar I told
you about
(Fill in the blanks with suitable articles, if
necessary)
(i) Give the verb forms from which the following nouns have been derived :
Foundation, Service, Reception, Success.
(j) Give the adjectival forms of the following :
Marvel, Wonder, Spectacle, Sorrow.
(For the candidates admitted from 2007 onwards) B.Sc. DEGREE EXAMINATION, JUNE 2008.
First Year
Part III Information Technology (SDE)
Allied I MATHEMATICAL FOUNDATIONS FOR COMPUTER SCIENCE
Time : Three hours Maximum : 100 marks
Answer any FIVE questions
1. (a) Evaluate:
|
1 + a, |
a2 |
a2 | |
|
a, |
1 T &2 | ||
|
ax |
a2 |
1 + a3 | |
|
ax |
az |
X+Ui |
(b) Solve the equation
2. (a) Define the rank of a matrix, (b) Find the rank of the matrix.
1 1 -1 1-1 2 3 10
Show that
1 2
3 -2
4 2
1
-1
1
3
1
1
(c)
(10)
A =
satisfies the equation A3 - 23A - 40/ = 0. Hence find A'1
Prove that union of sets and intersection of
3. (a)
(10)
(2)
Venn
(8)
(4)
sets are associative.
(b) Write De Morgan's laws.
Prove De Morgan's laws
Cc)
diagram.
4. (a)
(b)
following tautologies?
(i)
(ii)
using
What is tautology? Contradiction?
Construct the truth table for each of the formulae. Which of the formulae are
(16)
5. (a) Show that
(V x)(P (x)v Q (*)) => (v j:)P (x)v (3x)Q (x)
(b) Is the following conclusion validly derivable from the premises given?
If (v *)(/>(*)-<?(*)); (3 y)P(y), then (3 z)Q{z) (10)
6. (a) Write the definitions of
(i) one-to-one
(ii) onto
(iii) many-to-one
(iv) identify functions. (8)
(b) Write all possible functions from X = {1,2 } to y = {a, b, c } and classify them into one-to-one, onto, neither one-to-one nor onto types of functions. (12)
7. (a) Let G be an undirected graph. Then prove that G is bipartite iff it contains no odd cycle. (10)
(b) Show that a simple digraph is strongly connected iff there is a closed directed walk in G which includes each node atleast once and no isolated node.
(10)
Define the rank of a matrix. Find the rank of the matrix.
(a)
(b)
11-1 1 -1 2 3 10
Show that
1
-1
1
3
1
1
(c)
1 2
3 -2
4 2
(10)
A*
satisfies the equation A3 - 23A - 40/ = 0. Hence find A-'
Prove that union of sets and intersection of
3. (a) sets are associative.
(8)
(4)
Write De Morgans laws.
(b)
(c)
diagram.
4. (a)
(b)
following tautologies?
(i)
(ii)
Prove De Morgans laws using
What is tautology? Contradiction?
Construct the truth table for each of the formulae. Which of the formulae are
(16)
Oja
5. (a) Show that
(V x){P (x)v Q (x))=> (v x)P (x)v (3x)Q (x)
(10)
(b) Is the following conclusion validly derivable from the premises given?
If (V x) (P (x) Q (x)); (3 y) P (y), then (Sz)Q(z) (10)
6. (a) Write the definitions of
(i) one-to-one
(ii) onto
(iii) many-to-one
(iv) identify functions. (8)
(b) Write all possible functions from X = {1,2 } to y = {a,b,c } and classify them into one-to-one, onto, neither one-to-one nor onto types of functions. (12)
7. (a) Let G be an undirected graph. Then prove that G is bipartite iff it contains no odd cycle. (10)
(b) Show that a simple digraph is strongly connected iff there is a closed directed walk in G which includes each node atleast once and no isolated node.
(10)
8. Provo that the following statements are equivalent for a graph G with n vertices (n 12).
(a) G is a tree
(b) Any two distinct vertices of G are joined by a unique path
(c) G is minimally connected
(d) G is connected and has n -1 edges
(e) G is acyclic and has n -1 edges.
(4 + 4 + 4 + 4 + 4 = 20)
(For the candidates admitted from 20072008 onwards) B.Sc. DEGREE EXAMINATION, JUNE 2008.
First Year PART III Information Technology DIGITAL FUNDAMENTALS AND ARCHITECTURE Time : Three hours Maximum : 100 marks
Answer any FIVE questions.
(5 x 20 = 100)
1. (a) Convert the decimal number (5I2.5)l0 into equivalent binary, octal and hexadecimal numbers. (9)
(b) Explain about parallel binary adder with neat diagram. (6)
(c) Prove Demorgans theorem. (5>
2. (a) Explain BCD adder with diagram. (10)
(b) Implement the following Boolean expression using NAND gates only. Y = A+ BC+AC (10)
3. (a) Using Karnaugh map simplify the following :
f(A, B,CtD) = m, 3,5,6,7,9,11,13). (10)
(b) Write about synchronous counters. (10)
4. (a) Explain JK mastor-slave flip-flop. (10) (b) Write about multiplexers. (10)
5. (a) With neat diagram write about the architecture of 8085. (10)
(b) Write the addressing modes of 8085. (10)
6. (a) Explain Daisy-Chaining priority. (10) (b) Explain DMA controller. (10)
7. Illustrate the Virtual Memory Concept. (20)
8. Write a note on Main memory. (20)
(For the candidates admitted from 2007 onwards j B.Sc. DEGREE EXAMINATION, JUNE 2008.
First Year Part III Information Technology DATA STRUCTURES AND C PROGRAMMING Time : Three hours Maximum : 100 marks
Answer any FIVE questions.
1. Discuss about problem solving techniques.
2. Explain - Loop control statements.
3. Write about functions. Write a program to find the factorial a number using recursive functions.
4. What is meant by FILE? Discuss in detail about it.
5. (a) Differentiate structure and union with example.
fb) Explain about command line arguments.
6. Write about stack.
7. Short notes on :
(a) Doubly linked list.
(b) Insertion sort.
8. Explain different methods of Searching.
D 3004 Q.P. Code : [07 DSC 01]
(For the candidates admitted from 2007 onwards) B.Sc. DEGREE EXAMINATION, JUNE 2008.
First Year
Part III Computer Science
DIGITAL FUNDAMENTALS AND ARCHITECTURE
Time : Three hours Maximum : 100 marks
Answer any FIVE questions.
Each questions carries 20 marks.
(5 x 20 = 100)
1. (a) Convert (l0767)io to hexadecimal (2)
(b> Multiply (lA3)i by <89)i. (2)
(c) Explain in brief the functioning of parallel binary adder with its block diagram. (10)
(d) Why NAND gate is called as an universal
gate? Explain. (5)
2. (a) Reduce the following using mapping method inSOPfonn. (10)
L = xM(0,1,2, 3,4, 6,10(U,13)
(b) With its block diagram explain the functioning of a multiplexer. (10)
3. (a) Explain in brief the various addressing modes of 8085. (8)
(b) With the block diagram of Intel 8085, explain the functioning of various registers in it. (12)
4. Discuss in brief about asynchronous data transfer between independent units. (20)
5. (a) Explain in brief the three types of mapping procedures when considering the organization of cache memory. (15)
(b) Write in short about main memory. (5)
6. (a) Simplify the following :
(i) A+BC(A+WC) (5)
(ii) AIB+C(AJJ + AC)J. (5)
(b) Explain the functioning of a shift counter with its block diagram. (10)
7. (a) With the block diagram of DMA controller, explain the functioning of it. (10)
(b) Discuss briefly about Daisy chaining priority and parallel priority Interrupt. (10)
8. Explain the following :
(For the candidates admitted from 2007 onwards) B.Sc. DEGREE EXAMINATION. JUNE 2008.
First Year Part III Computer Science DATA STRUCTURES AND C PROGRAMMING Time : Three hours Maximum : 100 marks
Answer any FIVE questions.
All questions carry equal marks.
(5 x 20 = 100)
1. (a) Explain structure of a C program. (10)
(b) Expliiin various operators available in 'C'.
(10)
2. Write short notes about :
(a) Arrays (10)
(b) Macros (10)
3. Write C* language program for
(a) Printing of multiplication table. (10)
(b) Fibonacci series. (10)
4. (a) Discuss various preprocessor directives. (10)
(b) Explain various string functions available in *C\ (10)
5. Write short notes about:
(a) Enumerated data types. (10)
(b) Array of structure. (10)
6. Explain various operations on queue. (20)
7. Write procedure and sort the following data using Heap sort:
44, 55, 12, 42, 94, 18, 06, 62. (20)
8. (a) Discuss about Linear search and Binary search. (10)
(b) Quick sort algorithm. (10)
D 3513 Q.P. Code : [07 DBM 01/
(For the candidates admitted from 2007 onwards) B.B.M./B.B.A. DEGREE EXAMINATION, JUNE 2008.
First Year
Part III Business Management/Business Administration
MANAGEMENT PROCESS
Time : Three hours Maximum : 100 marks
Answer any FIVE questions.
Each question carries equal marks.
(5 x 20 = 100)
1. Define organization. Explain the factors to be considered in the establishment of an organization.
2. Describe the Elton mayos contributions to human relations approach.
3. Examine the merits and demerits or various types of planning.
4. What is functional organization? Give a detailed account of the merit and demerits of such an organization.
5. Briefly discuss about the recent trends and new perspectives in management.
6. What are the devices of control? Discuss about the special techniques of control.
7. Explain management and state its functions.
8. Decision making is the primary task of the management'. Discuss this statement and explain the process of decision making.
D 3514 Q.P. Code : [07 DBM 02/ 07 DBBA 02]
(For the candidates admitted from 2007 onwards)
B.B.M/B.B.A. DEGREE EXAMINATION, JUNE 2008.
First Year
Part III - Business Management/Business Administration
ACCOUNTING FOR MANAGERS
Time : Three hours Maximum : 100 marks
Answer any FIVE questions.
(5 x 20 = 100)
1. Explain the rules of the double entry system with example. Explain the advantages and disadvantages.
2. Prepare Ledger Accounts for the following transactions in the books of* :
Rs.
45.000
25.000
June 1 Started business with cash June 1 Paid into bank
|
June 2 |
Goods purchased for cash |
15,000 |
|
June 3 |
Purchase of furniture and payment by Cheque |
5,000 |
|
June 5 |
Sold goods to Y |
4,000 |
|
Juno 10 |
Goods purchased form Z |
7,000 |
|
June 18 |
Goods returned by Y |
200 |
|
June 21 |
Paid telephone rent for 1 year |
1,000 |
|
June 30 |
Paid for: | |
|
Stationary |
200 | |
|
Rent |
1,000 | |
|
Salaries for staff |
5,000 |
3. From the following Trail balance of Mr. X, prepare a Trading and Profit and Loss Account for the year ended on 31.12.2000 and balance sheet as on that date, after giving effect to the adjustments.
Dr. Cr.
Rs. Rs.
Capital 1,80,000
Drawing 32,500
Stock (on 1.1.2000) 1,74,460
Return Inwards 5,540
Carriage Inwards 12,400
Deposits with Mr. Y (Interest free) 13,750
Carriage Outward 7,250
Loan to Z@5% given on 1.1.2000 10,000
Return outward 8,400
Interest on the above loan 250
Rent 8,200
Rent outstanding 1,300
Purchases 11,29,700
Debtors 40,000
Good will 17,300
Creditors 30,000
Advertisement Expense 9,540
Provision for doubtful debts 12,000
Bad debts 4,000
Patents and trade marks 5,000
Cash in hand 620
Sales 12,79,140
Discount allowed 3,300
Wages 7,540
Plant and Machinery (purchased on 30,000 1.1.2000)
15,11,090 15,11,090
Adjustments :
(a) Increase bad debts by Rs. 6,000. Make provision for Doubtful Debts @ 10% and Provision for Discount on Debtors @ 5%.
(b) The value of the closing stock is Rs. 1,87,920
(c) Wages include Rs. 2,000 paid for the erection of Machinery on 1.1.2000
(d) Provide depreciation on machinery
@ 10% p.a.
4. Explain in detail the distinction between Cost Accounting and Management Accounting.
5. Explain the various classifications of cost with example.
6. Two materials, X and Y , are used as follows : Minimum usage : 50 units per week each, Maximum usage : 150 units per week each,
Normal usage : 100 units per week each,
Ordering quantities : X-600 units, and Y-1000 units Delivery period : X-4 to 6 weeks, Y-2 to 4 weeks
(a) Minimum level
(b) Maximum level
(c) Ordering level
7. Standard time allotted for a job is 20 hours anci rate per hour is Rs. 2 plus a dearness allowance @ 5( paise per hour worked.
The actual time taken by a worker is 15 hours. Calculate the earnings under (a) Time system b. Piec* wage system (c) Halsey Plan (d) Rowan Scheme
8. Prepare a flexible budget for the overheads on thc-basis of the following data. Ascertain the overhead rates at 50%, 60% and 70% capacity.
|
Variable overheads: Indirect material Indirect labour |
At 60% Capacity Rs. 6,000 18,000 |
.Semi-variable overheads:
Electricity (40% fixed 60% variable) Repairs (80% lixed 20% variable)
S0r000
3,000
Fixed overheads:
Depreciation 16,500
Insurance 4,500
Salaries 15,000
TotaJ overheads 93,000
Estimated direct labour hours 1,86,000
(For the candidates admitted from 2007 onwards)
B.B.M7B.B.A. DEGREE EXAMINATION, JUNE 2008.
First Year
Part III Business Management /
Business Administration
Allied MATHEMATICS FOR MANAGEMENT
Time ; Three hours Maximum : 100 marks
Answer any FIVE questions.
(5x20 = 100)
1. A salesman visits 274 housewives in a town to find out their views about three products A, B and C. He finds that 157 use A, 98 use only A, 22 use all the three, 14 use A and C but not B, 39 use B and C, 48 use only B.
(a) Which product is most popular to his inquiry?
(b) How many use produce C only?
(c) What fraction use atleast two products?
(d) What percent use only one of the products?
'2 3 4 *
3 2 1 i 1 -2
3. A man repays a loan of Rs. 3,250 by paying Rs. 20 in the first month and then increases the payment by Rs. 15 every month. How long will it take to clear his loan?
4. Discuss the various types of classifications of data with example.
5. Define AM, GM, HM. Explain its merits and demerits.
6. Calculate the Mean, Median and Mode of the following:
|
Class |
Frequency |
|
1-10 |
3 |
|
11-20 |
7 |
|
21-30 |
13 |
|
31-40 |
17 |
|
41-50 |
12 |
Class Frequency
61-60
61-70
71-80
81-90
91-100
10
8
8
6
6
7. Ten competitors in a beauty contest are ranked by three judges in the following order :
Judge 1:14632978 10 5 Judge 2: 26547 10 9381
Judge 3: 3745 10 89261
Use Rank correlation coefficient to determine which pair of Judges have the nearest approach to common taste in beauty.
8. Explain any four methods of finding trend in a time series.
(For the candidates admitted from 2007 onwards)
B.Sc. DEGREE EXAMINATION, JUNE 2008.
First Year
Part III Mathematics
TRIGONOMETRY, VECTOR CALCULUS AND ANALYTICAL GEOMETRY
Time : Three hours Maximum : 100 marks
Answer any FIVE questions.
(5 x 20 = 100)
1. (a) Prove that
32 cos6 9 = cos 60 + 6 cos 40 + 15 cos 20 + 10.
(b) If sin (& + i fi) = tan a + i sec a, then prove that cos 20 cosh 2 = 3.
(c&;) 32 cos6 0 = cos 60 i 6 cos 40 h 15 cos 20 + 10 601 jSlgf&jA.
(*%) sin (O + i fi) tan a + i sec a, sroiflo;
cos 20 cosh 2<p = 3 cran riprrgaia
2. (a) Prove that:
log tan + j = i tan"1 (sinh x).
(b) Find the sum of the series :
sin a + sin (a + p) + sin {a + 2fi) + -
log tan *tan_I (sinh *).
(3b) Messrs.
log tan = i tan'1 (sinh jc).
3. (a) Prove that
{i) Vx (u x i7)= (u v)u - (v u)v
- [(u V)y - (V w)].
(ii) dio curl F = 0.
<b) Prove that:
U?N) jlfp|6ijA:
(i) Vx (rT x v) = (tT V)u - (V u)u [( -iy 5* )]
(ii) div curl F = 0,
(<=&) %6m:
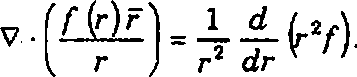
4. (a) Verify divergence theorem for
F = xi+yj + zk over the region bounded by x - 0, x = a, y-0, y ~ a, z- 0, z ~ a.
(b) Verify Stokes theorem for F = y i + z j + x k over the surface of the hemisphere x2+y2+z2 = 1 above the x o y plane.
(i) F - x i + y j + zk x = 0, x = a, y - 0, y~a, 2 = 0, = a u(g>luSla)
cSlfflcu Gji)jD#l>T iflu(rnraih.
($>) 3 ? * + 2 ; + * A x o y npflm i&Qvnen x2 + y2 + z2 = 1 hTaijp nrr <5fT6TTi LifDupuiSlan i6gy QuCu.fr$is! GjifpeDerr ffftuimasajib.
5. (a) Obtain the Fourier series for the function f (x)- x, - n < x < n.
(b) Find half-range Fourier sine series for f (*) = x (x - x), 0 < x < x.
(<<) f (x) = x, -x <x < n sresriD $rrnrL|*frn y.fflujn
rflujiT t Qfrt_ngft anewra.
6. (a) Derive the polar equation of a conic.
(b) Find the equation of the chord joining the points whose vectorial angles are a - /? and a + fi on the conic.
(cSn) 90 Avlbq Qsui_l|.uS!67T $|0U ffUjOTlUdL.lrf.GDCn
060.
QcuLuj.uSin iSgjerrai a-/3 u>jbpu) a + /?
cuonGu Ga;rTOTfij&nfr Q&irewn i_|d7cift<9i5>6n
@er>6KT(5Lb prrOTflssr tDOTurr fT6wr*.
7. (a) Kind die shortest distance between the lines
x-Z y-8 z-3 , x-i-3 y+ 7 z-6
-= ---and -* ----.
3-11 -3 2 4
(b) Find the equation of th<; spheres which pass through the circle xl hy2 + z2 * 5, x + 2y + Zz 3 and touch the plane 4* + 3y = 15.
, . *-3 v-8 2-3 . . **3 y+7 *-6
(9j) ----=- togjrau) = iSLL = zz.
V ' 3 -1 1-32 4
4,1 uj @65)i_GiuujrT2r iBsilgy
6jfTW0l$>.
xzf/ i zr 5, * + 2y~3z=3 crtwo euL-i_>iT ejlttjiris <3v>cufr*6qii> LorQipiib 4x + Sy 15 ctsmjd Q0fr(jjugrr6qih s..cjtft Cnctfijaerflwr aLDCTTurrCfeertff, rrswr*.
8. (a) Find the equation of the cone whose vertex is (l,-2,3) and the guiding curve is x2 +yi + z'2 = 25,
Z a 2.
'b) Find tho equation of the right circular cylinder whose axis is x = 2y = -e and radius 4.
(l - 2,3) Gronucn# (ipC5>63tujffQi:b LOpipub x* +.Y2 + *3 ~ 25, z- 2 6rnucn &jySIrTC(TJ
j$f>OT<a;a?><ru-jrra|ib oubiSlan $u>nuir (iji ttrrafeiai.
Reg. No.:.........................................
(c&) x = 2y = -z srenu&ip, effirsajib tuippLb ijtb
4 ,ibQa>frTu (oj&ir qjCl. peosrruSlerT tfio5Tufr(j) arrears.
\y
D 3136 Q.P. Code : [07 DMA 03]
(For the candidates admitted from 2007 onwards) B.Sc. DEGREE EXAMINATION, JUNE 2008.
First Year Part III Mathematics Allied : STATISTICS FOR MATHEMATICS Time : Three hours Maximum : 100 marks
Answer any FIVE questions.
(5 x 20 = 100)
1. (a) A random variable X has the following probability function:
x: 0123456 7 pU): 0 K 2K 2K 3K K2 2K2 7K*+K
Find K and P (0 < X < 5).
(b) Find the mean and variance of the distribution whose probability density function is f(x) = y0 *(2-4 0 < * < 2.
(c) State and prove addition theorem on expectation.
(<i) t3anGu0ib ?(mt)p( K,
P (0 < X < 5) ujcufpenfD rrOTr :
x: 01234 56 7 p(x): 0 K 2K 2K 3K K> 2K* 1$P+K
() uijueSlgjr i_rr$<j nirq
/(x) = y0 x(2 - x\ 0 x 2 srejflcu 5crfr*iflDUJU-|ib
ui7un)uti).f>ujiqtb &>(T6Wt,.
(gi) TlfTunoS)ai jSjpajff*.
2. (a) If xi,x2l- ' ,xn arc independent random variables, show that
M,{(f) = Mx> (t)- Mx,((>M,. (t).
(b) If 'M=j 0, therwise j find Var(x) and Var(K).
(c) State and prove Chebychevs inequality.
(5H) xltx2,'" ,xn 6TOIU5)6U ffffniS&QMT SlDOjrriUUH lafrrflaer crefleb
M,(t) = MXi (0-(0- M,' (t) ST65ia>
* \ / ( \ (2-x~y, OZx l,OSy ll
(-$>) f(x>y)=\ A \t<ST&Q)
[ 0, u>{Djpu. J
Var(X) ujjbgjjib Var (K)gj fiewr*.
(@) QffiSK8tffilw ffujft6ineou>>uj a*.f$ ilg*64.
3. (a) Find the density function f (*) corresponding to the characteristic function
(b) Find the M.G.F. of X and mean from the following distribution :
P(X =r) = q'-1ptr = 1,2,-
(c) State and prove weak law of large numbers.
(<3h) PJ=| | i |> 1 J 6*TU* UGWTU6Tf)Qj
rriTL| CTerfld) @0ji)($ QfTi_iTq6y)i_aj jly?4 sffniS)>en 8>nGSin&.
{*%,) X -err Qu0<$# Qrrena CL06uffa<$u> rriTLj u3fbgstx> (7rrif)a)uj i$e5T6U0ib i_H7Cug*}<$ arrema :
P(X=r) = q'-'p,r = 1,2,-(j) Quifluj (large) er*r<g$*airffr fc.gy$ujfb0) gS10gshli
6*v())
4. (a) If the mean and variance of binomial
distribution are 4 and , find P (X > l).
3
(b) Find the M.G.F. of a binomial distribution and hence find the variance.
(c) Show that for a normal distribution
= 1-3-5 (2/1 -l)<TS" .
(t) rr<5g|LJL| uijeueftsn icpnjitb uijeufbuu|.
qP)jdCiij 4 tofbpii) , crfla> P l) gj asrrewra.
3
(>) rr0gaui_| uijcugSIwt Qu0ft<$Qne&A ft.0airr*<$ib sfrnreau irewr. cuturr* urjeujDutenuj frcwr.
2n - 1 3 5 (2/1 - l) cr2n OTCTTafTU*.
5. (a) Seven coins are tossed and number of heads noted as below. Fit a binomial distribution if the nature of the coin is unknown.
No. of heads: 01234567 Frequencies: 7 6 19 35 30 23 7 1
(b) Show that -rAjr + for a Poisson
dA
distribution.
(c) Show that fr a normal distribution.
(<l) 5T(Lp J&fTfiKTUJtijSOT eSffUUll CTesrr5Tuu@$jD|. jBir5Tujj)ai thd QiflajnCunj i5ljT6U0ii> nnjgjuq ui?eu>co Quit0$j& :
aa>6iT CT5T6wf1*ej)ffi: 0 X 234567 cfxoQ&iGBrasdr: 7 6 19 35 30 23 7 1
{>) urriuswrrofT uij6ugijs<3j Mr*i =rMr-i'''~TL
dX
CTT<&srTil@.
() @u-io>j)>a> uijugjft@ //2rt+ j = 0 CTn**nu.
6. (a) State and prove additive property of X1 distribution.
(b) Derivet the probability density function of /'-distribution.
(c) Write the four applications of -distribution, (c&l) X2 U76U$T *vL_@UUr>U *fcll
(<) F- uijeusSlesT ji*hitc5>u $0cSI.
(@) t - urjajeSrin utuanufrQawn f$fTT<fi>5T er(jgji.
7. (a) Derive the probability density function of X1 distribution.
(b) Find ii2f for /-distribution and hence find f$%.
(&;) X2 - ' ui7GUyn {&)y>eq Hi-#)6 9iTfra>u
(5)6$ *
{*$>} fjfy. gj *fT6Mra. @aj6u$ujrT* fi2 gj
fT5T.
8. (a) Fit a curve of the form yabs for the following data :
x: 12345678 y: 1.0 1.2 1.8 2.5 3.6 4.7 6.6 9.1
(b) If V(Y) = 9 and the lines of regression are 4x-6y + 330. 20x-9y-107 = 0, find
(i) the means of x and y.
(ii) correlation coefficient between x and y.
(iii) standard deviation ofy.
(eS*0 iSlrroj(5u> Slur;rij(CTF,*0 y = abx *rsi0) <sunsrrj6?>f75>uj Oungj* :
*: 12345678 y: 1.0 1.2 1.8 2.5 3.6 4.7 6.6 9.1
(=&) v(x-)= u>njpu> 4x-5y + 33 = 0, 20x -9>' -107 = 0 ct!u5)u e_i_sn Q$nLjrL| (S*rT($)*n gt5o idnu0ucr;upenrp anwa :
(i) x iDffrgiiby - ctt sijfrsifl.
(ii) x icpgyib y&Q eoi_Cuj o.cireT
(iii) y-en $l.l_ efito&aib.
D 3149 Q.P. Code : [07 DOT 01J
(For the candidates admitted from 2007 onwards) B.Sc. DEGREE EXAMINATION, JUNE 2008.
First Year
Part III Catering Science and Hotel Management FOOD PRODUCTION AND PATISSERIE I Time : Three hours Maximum : 100 marks
Answer any FIVE questions.
Each question carries 20 marks each.
(5 x 20 = 100)
1. Explain the aims and objects of cooking food.
2. What are the various methods of preparing ingredients before cooking?
3. List out the various staff of the kitchen and explain their duties and responsibilities.
4. Classify soup and explain each with two examples each.
5. Classify vegetables and gives suitable uses of each.
6. Explain the role of raising agents in cookery.
7. With the help of a diagram explain the cuts of chicken and its uses.
8. List the various equipments used in the kitchen mention their uses and maintenance.
(For the candidates admitted from 2007 onwards) B.Sc. DEGREE EXAMINATION, JUNE 2008.
First Year
Part III Catering Science and Hotel Management FOOD AND BEVERAGE SERVICE I Time : Three hours Maximum : 100 marks
Answer any FIVE questions.
Each question carries 20 marks.
(5 x 20 = 100)
1. List out the various catering establishment and write a note on each.
2. Draw the organisation chart of the restaurant and explain the duties of each staff.
3. Write notes on the following :
(a) Pantry
(b) Misen place
(c) Dummy waiter
(d) Coffee shop.
4. Explain the French classical men with courses and examples.
5. What is a beverage? Classify with examples.
6. Write an elaborate note on ice-creams.
7. Explain the order taking procedure in
(a) restaurant (b) room service.
8. Explain the qualities of a good waiter.
(For the candidates admitted from 2007 onwards) B.Sc. DEGREE EXAMINATION, JUNE 2008.
First Year
Part III Catering Science and Hotel Management ACCOMMODATION OPERATIONS Time : Three hours Maximum : 100 marks
Answer any FIVE questions.
Each question carries 20 marks.
(5 x20=100)
1. Explain the importance of housekeeping department in a hotel.
2. What aro cleaning ag<;nts and cleaning equipments. Explain them in detail.
3. Draw the layout of a linen room and explain the activities in a tinen room.
4. Draw the hierarchy chart of the house keeping department and explain the duties of each staff.
5. Define Hotel. Classify hotels and explain.
6. List the various Front office staff in a large hotels and mention their duties.
7. With a flow chart explain the process from reservation unit check in and check out.
8. Explain the accounting system in a large hotel.
(For the candidates admitted from 2007 onwards)
P.G. DIPLOMA EXAMINATION, JUNE 2008.
First Year
Part III Optometries
GENERAL PHYSIOLOGY
Time : Three hours Maximum : 100 marks
SECTION A (20 x 1 = 20 marks)
Answer ALL questions.
Select the most appropriate answer from the answers
given.
1. Memolytic aneamia may result from
(a) Transfusion reaction
(b) Sickle cell
(c) Abnormal heart valve
(d) Iron deficiency.
2. The ribosome free endoplasmic reticulum plays a role in each of the following Except
(a) Synthesis of lipid
(b) Synthesis of protein
(c) Detoxification
(d) Glycogenolysis.
3. Mitochondria
(a) Contain DNA and ribosomes
(b) Contain enzyme associated with krebs cycle
(c) Are capable of selfreplication
(d) Derive energy from fatty acid.
4. Injury to motor nerve supplying skeletal muscles causes, muscle
(a) Paralysis (b) Atrophy
(c) Fibrillation (d) Fasciculation.
5. Following are the plasma proteins Except
(a) Fibrinogen (b) Albumin
(c) Globulin (d) Myosin.
6. Pacemaker of heart is present in
(a) Aorta (b) Right atrium
(c) Left atrium (d) Left ventricle.
7. Smooth muscle does not contain
(a) Actin (b) Myosin
(c) Troponin (d) Tropomyosin.
8. Aldosterone excess produce
(a) Hypematri uri a (b) Hypokalemia (c) Tetany (d) All of the above.
9. Climacteric is
(a) Female menopause
(b) Male menopause
(c) Emotional disturbance
(d) Loss of Libido.
10. Ovulation.to occur, which hormone is essential?
(a) FSH (b) LH
(c) Oestrogen (d) Progesterone.
11. Organ ofcorti is located on
(a) Basilar membrane
(b) Reissners membrane
(c) Tectorial membrane
(d) Reticular Lamina.
12. Diabetes Melitus is due to the deficiency of
(a) ADH (b) Insulin
(c) Cortisol (d) Glucagen.
13. Pancreatic juice contain all of the following Except
(a) Enzymes (b) Water
(c) Hormones (d) Bicarbonates.
14. The major contribution of semon is
(a) Testes (b) Epididymus
<c) Prostate (d) Seminal vesicle.
15. The normal heart rate is
(a) 60 beats/min (b) 70 beats/min
Cc) 100 beata/min (d) 150 beats/min
16. Respiratory centers are present in
(a) Brain stem <b) Cortex
(c) Cerebellum (d) Spinal cord.
17. Tactile sensibility includes each of the following Except
{a) Tactile discrimination
(b) Tactile localisation
(c) Appreciation of Temperature
(d) Appreciation of pressure.
18. Virus causing AIDS resides within
(a) T-lymphocytes (b) Plasma cells
(c) B- lymphocytes (d) Monocytes.
19. Injury in the primary auditory cortex may causc disability in
(a) Detecting loud sound
(b) I/Ocaiyzing sound in space
(c) Discriminating pitch
(d) Detecting sound pattern.
20. Gustation involves each of the following Except
(a) Foliate papillae
(b) Circum vallate papillae
(c) Fungiform papillae
(d) Filiform papillae.
SECTION B (5 x 6 = 30 marks)
Answer short questions.
21. (a) Homeostasis.
Or
(bl Krebtf cycle.
22. I'al Composition of blood.
Or
ib) Rh factor.
23. (a; Excitation contraction coupling.
Or
b) Mechanism of inspiration.
24. (a) Factors affecting GFFL
Or
(b) Functions of Limbic system.
25. (a) Taste buds.
Or
(b) Puberty.
SECTION C (5 x 10 a 50 marks)
Answer Essay on.
26. (a) Classify leukocytes and explain the characteristic features of lymphocytes.
Or
(b) Explain the functions of plasma proteins.
27. (a) Describe the events occurin in one cardiac cycle.
Or
(b) Describe the composition and functions cf saliva.
28. (a) Enumerate the functions of Liver.
Or
(b) Explain the transport of oxygen from lungs to tissue.
29. (a) Explain the mechanism of reabsorption of glucose.
Or
(b) Name the hormones of adrenal cortex and explain the actions of cortisol.
30. (a) With neat diagram explain the visual pathway.
Or
(b) Describe the stages of spermatogenesis.
DEGREE EXAMINATION, JUNE 2008. First Year Part III Optometries OPTICS AND REFRACTION
For the candidates admitted from 2007 onwards)
|
(For ti |
 |
Maximum: 100 marks
Time : Three hours
Answer ALL questions.
SECTION A (20 x 1 = 20 marks)
Objective type :
Blurring of vision for near work occurs in (a; hypermetropia (b) presbyopia
1.
(c) both of the above (d) none of the above.
Optical conditions of Aphakia include all EXCEPT
(a) loss of accommodation (b> astigmatism against rule
(c) enlargement of retinal image
(d) myopia.
3. Unilateral Aphakia can be treated by
(a) contact lens
(b) intraocular lens implant
(c) both
(d) none.
4. A newborn is invariably
(a) hypermetropic (b) myopic
(c) astigmatic (d) aphakic.
5. Astigmatism is a type of
(a) axial ametropia
(b) index ametropia
(c) curvature ametropia
(d) spherical aberration.
6. Hypermetropia causes
(a) divergent squint
(b) convergent squint
(c) both of the above
(d) none of the above
7. !n Retinoscopy using a plane mirror, when the mirror is tilted to the right the shadow in the pupil moves to the left in
(a) Hypermetropia
(b) Myopia more than -1 D
(c) Emmetropia
(d) Myopia less than -1 D.
8. Optica] condition of the eye in which refraction of the two eyes differs is
(a) Mixed astigmatism
(b) Irregular astigmatism
(c) Anisometropia
(d) Compound astigmatism.
9. Latent hypermetropia is detected when following mydriatic is used
(a) Adrenaline
(b) Phenylephrine
(c) Cyclopentolate
(d) Atropine.
10. Radial keratotomy is useful in
(a) Myopia (b) Hypermetropia
(c) Presbyopia (d) Aphakia.
11. Incident parallel rays come to a focus posterior to the light sensitive layer of retina in
(a) Aphakia
(b) Hypermetropia
(c) Both of the above
(d) None of the above.
12. The complications of myopia include all EXCEPT
(a) vitreous degeneration
(b) retinal detachment
(c) cataract
(d) closed angle glaucoma.
13. Indistinct distant vision is seen in
(a) Presbyopia
(b) Myopia
(c) Hypermetropia
(d) None of the above.
14. Contact lenses may be useful in treatment of all EXCEPT
(a) Keratoconus
(b) Refractive anisometropia
(c) Fuchs endothelial dystrophy
(d) Severe keratoconjunctivitis sicca.
15. Hard contact lens is made up of
(a) HEMA (c) PVP
(b) PMMA
(d> PVC.
16. Biconvex lens is used in all EXCEPT
(a) Aphakia
(b) Presbyopia
(c) Astigmatism
(d) Hypermotropia.
17. Determination of the refraction is done by all
EXCEPT
(a) Retinoscopy
(b) Refractomefcer
(c) Keratometer
(d) Perimeter.
18. Drug of choice-for pupillary dilatation in children is
(a) Atropine
(b) Homatropine
(c) Scopolamine
(d) Cyclopentolate.
19. Frequent change of presbyopic glasses is an early symptom of
(a) Closed angle glaucoma
(b) Open angle glaucoma
(c) Senile cataract
(d) After cataract.
20. Accommodation is maximum in
(a) Childhood
(b) Adulthood
(c) Middle-age
(d) Old-age.
Short Questions :
21. Describe refraction by prisms and uses of prisms.
22. Refraction in pseudophakia.
23. Danders reduced eye.
24. Subjective verification of refraction.
25. Best form lenses.
SECTION C (5 x 10 = 50 marks)
Long Questions :
26. Describe in detail optics of cylindrical lenses.
27. Physiological optical defects of the eye.
28. What is astigmatism, describe sturms conoid and correction of astigmatism.
29. Objective methods of refraction.
30. Describe the various forms of contact lenses and fitting of contact lenses in keratoconus.
(For the candidates admitted from 2007-2008 onwards) B.C.A. DEGREE EXAMINATION, JUNE 2008.
First Year
Part III Computer Applications DIGITAL FUNDAMENTAL AND ARCHITECTURE Time : Three hours Maximum : 100 marks
Answer any FIVE questions.
(5 x20 = 100)
1. (a) Convert the following :
(i) (63718)!0 to binary and hexadecimal.
(:>)
(ii) Prove De Morgans theorem. (5)
(b) Explain the working of BCD adder with a neat diagram. (10)
2. (a) Explain the following :
(i) Full Adder. (6)
{ii) XOR Gate. (4)
(b) Sketch the working of Shift Right register.
(10)
3. (a) Simplify the Boolean function.
f{A, B,C, D) =2X0, 2. 3, 5, 6, 7, 8, 9) and 10. II, 12, 13,14, 15 as dont cares. (6)
(b) Prove {A + BC +C)C = ABC +ABC + ABC using Boolean Algebra. f*t)
(c) Discuss the concept of multiplexer in detail.
(10)
4. (a) Explain the architecture of microprocessor in detail. (10)
(b) Write a note on input/output schemes. (10)
5. Explain the concept of priority interrupt. (20)
6. Discuss the working of asynchronous data transfer in detail. (20)
7. Explain the following :
(a) Programmable Peripheral Interface. (10)
(b) Programmable Interrupt Controller. (10)
8. Explain the concept of Associative Memory in detail. (20)
E 3005 Q.P. Code : [07 DSCA 03]
("or the candidates admitted from 2007-2008 onwards) B.C.A. DEGREE EXAMINATION, JUNE 2008. First Year
Part III Computer Applications
Allied I COMPUTER ORIENTED NUMERICAL AND STATISTICAL METHODS
Time . Three hours Maximum : 100 marks
Answer any FrVE questions.
1. la) Find the root of x3-3a:-5 = 0 by Regula Falsi method. (30)
(b) Solve the following system by Gauss Elimination Method. (10)
x, -x2+x3 ~l
+2x.j -3x3 = -6 2*j -5x2 +4xs = 5
2. Find the values of sinl8 and sin45 from the following table : (20)
: 0 10 20 30 40
y = cosx : 1.000 0.9848 0.9397 0.8660 0.7660
3. (a) Given the table ;
x: 0 0.1 0.2 0.3 0.4 : 1 1.1052 1.2214 1.3499 1.4918
Find the value of y ~ ex when x = 0.38 . (10)
(b) Using Lagranges interpolation formula, find the equation of the cubic curve that passes through the points (-1, -8), (0, 3) (2, 1) and (3, 2). (10)
4. Compute the mode from the following series : (20) Size of item: 0-5 5-10 10-15 15-20 20-25 Frequency: 20 24 32 28 20 Size of item: 25-30 30-35 35*40 40-45 Frequency: 16 34 10 8
5. From the prices of shares X and Y given below, state which share is more stable in value : (20)
X: 55 54 52 53 56 58 52 50 51 49
Y: 108 107 105 105 106 107 104 103 104 101
6. Calculate correlation coefficient and regression coefficient for the following data : (20)
X: 2 4 6 8 10 12 14 V: 4 2 5 10 4 11 12
Find the estimate ofy when x = 13.
7. (a) Evaluate -Jl2 to four decimal places by Newton-Raphson method. (10)
(b) Solve the system of equations :
8x-y + z-18 = 0, 2x + 5y-22-3 = 0 ; x + y-3z+6 = 0. (10)
8. Find y(0.1), y(0.2) given y' = x-2y y(0)-1 taking k - 0.1 by fourth order R.K. method. (20)
3 D 3003
|
Attachment: |
| Earning: Approval pending. |
