Anna University Chennai 2003 B.Tech Plastic and Polymer Engineering , IL/ - Question Paper

D 359

B.Tech. DEGREE EXAMINATION, APRIL/MAY 2003.

Fourth Semester

Polymer Technology

PM 401 MATHEMATICS IV

Time : Three hours Maximum : 100 marks

Answer ALL questions.

PART A (10 2 = 20 marks)

1.         Define geometric distribution and find its mean.

2.         State Chebyshevs inequality.

3.         Explain the terms : Basic feasible solution, optimal solution and degenerate solution of a L.P.P.

4.         How are the alternate optimal solution and unbounded solution inferred from the simplex procedure of solving a L.P.P?

5.         Write down the dual of the following L.P.P :

             Max.

             Subject to

            

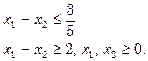
6.         Prove that the optimal solution of a transportation problem remains unchanged if all the elements of the cost matrix are increased or decreased by the same amount.

7.         Prove that , where n > 0.

8.         Distinguish between an ordinary point and a singular point of a second order linear ordinary differential equation.

9.         If , prove that .

10.      Solve for from : given that .

PART B (5 16 = 80 marks)

11.      (i) Find the moment generating function of the exponential distribution.
Find also its mean and variance.

             (ii) Suppose that a continuous random variable has pdf :

             Find the pdf of .

             (iii) Find the probability that atmost 5 defective fuses will be found in a box of 200 fuses if experience shows that 2% of such fuses are defective.

12.      (a) (i) Solve graphically :

             Min.

             Subject to :

            

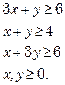
             (ii) Using simplex method, solve the following L.P.P :

             Max.

             Subject to :

            

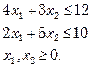
Or

             (b) (i) Formulate the following problem as a L.P.P :

             The manager of a milk dairy decides that each cow should get
atleast 15 units, 20 units and 24 units of nutrients and
daily respectively. Two varieties of feed are available. In feed of
variety 1, the contents of nutrients and are respectively
1, 2, 3 units per kg while for the variety 2, they are 3, 2, 2
respectively. The costs of varieties 1 and 2 are respectively Rs. 2 and
Rs. 3 per kg. How much of feed of each variety should be
purchased to feed a cow daily so that the expenditure is
minimised?

             (ii) Using BigM method, solve :

             Min.

             Subject to :

            

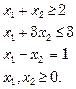
13.      (a) (i) Using duality theory, solve :

             Max.

             Subject to :

            

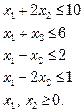
             (ii) Solve the following transportation problem with the unit cost
matrix as shown :

Or

             (b) (i) Find the optimal solution of the following L.P.P, by solving its dual :

             Max.

             Subject to :

            

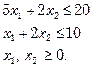
             (ii) A department has 4 subordinates and 4 tasks are to be performed.
The estimate of time (in hours) each person would take to perform
each task is given below :

             How should the tasks be allotted to the persons so as to minimise
the total personhours?

14.      (a) (i) Prove that .

             (ii) Prove that is an ordinary point of and solve the differential equation in series.

Or

             (b) (i) Evaluate , using Gamma functions.

             (ii) Prove that is a regular singular point of :

             and find its most general series solution.

15.      (a) (i) Define Ztransform. Find .

             (ii) Find the general solution of the following difference equation :

.

Or

             (b) (i) Prove that .

             (ii) Find .

             (iii) Solve using Ztransform :

             given that