Bengal Engineering and Science University 2006 B.E Computer Science and Engineering Network and Transmission Lines - Question Paper
the ques. paper is with the attachment.
Ex/BESUS/ EE-407/ 06 B.E. (CST) Part-II 4th Semester Examination, 2006
Network and Transmission Lines
Time : 3 hours Full Marks : 100
Use separate answerscript _for each half.
Answer SIX questions taken THREE _ from each half.
Two marks are reserved_for neatness in each half.
FIRST HALF
1. a) From the definition of Laplace transformation, prove that:
where all symbols carry their usual meanings. b) Obtain Laplace transform of the rectangular pulse shown in Fig. 1. 9+7
I'O
Fig.l
2. a) State and prove the Initial value and Final value theorems in Laplace transformation.
b)
|
.C |
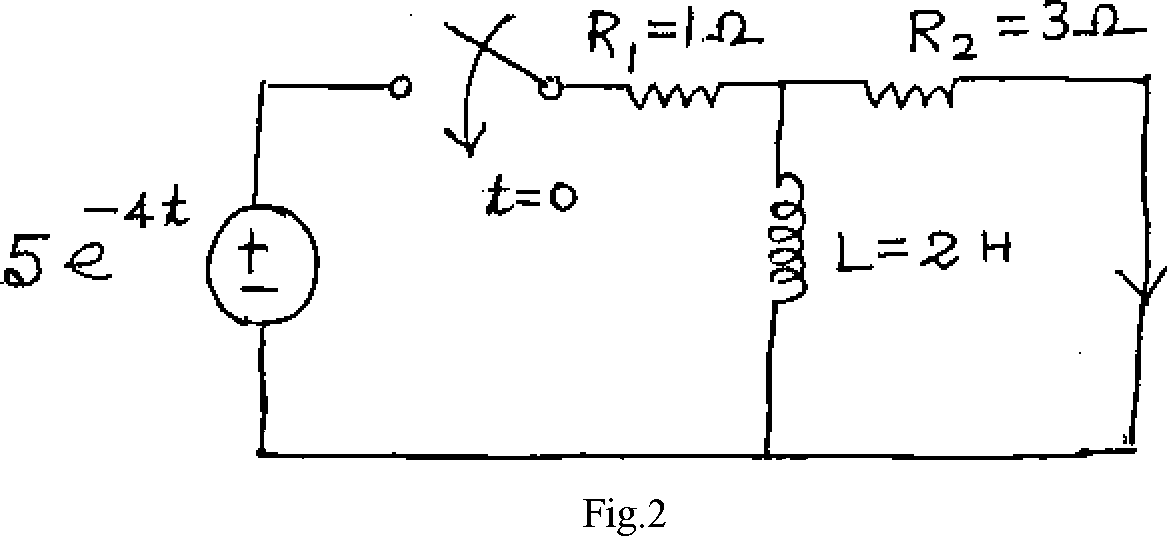 |
The circuit shown in Fig.2 was initially at rest. The switch S is suddenly closed at t = 0. Determine the current i2(t) using Laplace transformation. 8+8
b) A rectangular pulse of 2 sec. duration as shown in Fig.3(a) is applied to the circuit of Fig.3(b), which was initially at rest, at t=0. Using Laplace transformation method find out the voltage Vc (t) across the capacitor and sketch the wave form.
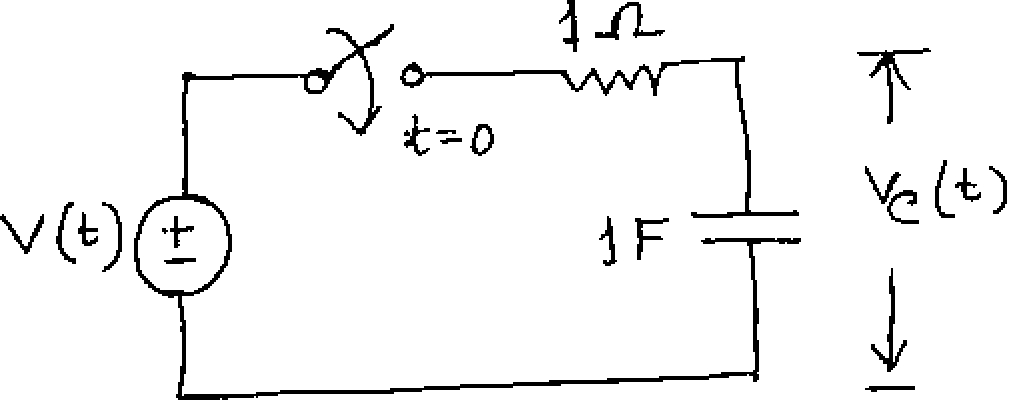 |
|
Fig.3 |
7+9
4. a) What is the characteristic impedance of a filter? Obtain the characteristic impedance for a prototype T-type filter in terms of reactance values of the filter arms.
b) What is cut-off frequency of a filter? Derive the expression for cut-off frequency for a prototype low pass filter. 8+8
a) What is attenuation constant (a) and phase shift constant (P) of a filter?
b) Derive the expressions for attenuation and phase shift in a prototype high pass filter in its pass band and attenuation band. 6+10
6. a) Derive an expression for characteristic impedance of a transmission line. How does the expression for it change when the line is lossless?
b) Derive an expression relating the propagation constant with primary constants of a transmission line.
c) Write down expressions for current and voltage at any point at a distance "x" from the sending end of a line using "Line Equations" (derivation not needed) and obtain the values of constants used in line equations when the conditions at the sending end are known.
d) Assuming the expressions for "line equations" obtain the value of the input impedance of a line in terms of exponential form (derivation of line equations not needed). 4x4
7. a) Calculate the primary constants of a transmission line having
(Zo) = 710 Z-14.240 ohm and y (gamma) = 0.0185 Z74.810 at f= 1 kHz.
b) The permissible approximations for unloaded underground cable at audio frequency are coC G and coL R. Calculate the characteristic impedance, attenuation and phare constants. Also find the velocity of propagation.
c) Analytically establish the characteristics of a high frequency transmission line.
6+6+4
8. a) What is reflection coefficient? Derive a relation between the reflection
coefficient and voltage standing wave ratio.
b) A section of HF lossless transmission line is (0.4X,) long and is terminated in a short circuit the characteristic impedance of the line is 73 ohms; determine the input impedance of the line section at operating frequency of 200 MHz. Deduce the necessary formula used.
c) Derive the expression of the reactance to be inserted in an ordinary shunt equalizer. What is its use? 4+8+4
9. a) A pair of two port networks are connected in cascade. Show that the overall
ABCD parameter network matrix is the matrix product of ABCD parameter matrices of individual networks.
b) Obtain the expressions of input and output impedances of a two port network in terms of transmission parameters.
c) Find Z-parameters of a lattice network assuming the series arm impedance to be Z] ohm (each) while the diagonal impedence is Z2 ohm (each). 5+5+6
10. a) Write short notes on (any two) : i)
Concept of inverse network ii) Stub matching in transmission line iii)
Loading of lines
b) The currents Ij and I2 at input and output port unsymmetrical two port network ("pi" configuration) is expressed as
I] = 5 V, - V2 and I2 = -V2 + V,. Assuming Yj and Y2 to be the shunt arm admittances while Y3 is the series arm admittance of the "pi" network, find the values of Y|, Y2 and Y3. Find also the input impedance of the given circuit when a load of (3 + j 5) ohms is connected across the output port. 4 x 2+8
|
Attachment: |
| Earning: Approval pending. |
